机器学习复习资料
大纲复习资料
第一章 机器学习简介
机器学习的概念、要素、类型
概念
机器学习(Machine Learning,ML)是指从有限的观测数据中学习(或“猜测”)出具有一般性的规律,并将这些规律应用到未观测数据样本上的方法。主要研究内容是学习算法。
机器学习(英语:machine learning)是人工智能的一个分支。机器学习理论主要是设计和分析一些让计算机可以自动学习的算法。机器学习算法是一类从数据]中自动分析获得规律,并利用规律对未知数据进行预测的算法。因为学习算法中涉及了大量的统计学理论,机器学习与推断统计学联系尤为密切,也被称为统计学习理论。算法设计方面,机器学习理论关注可以实现的,行之有效的学习算法(要防止错误累积)。很多推论问题属于非程序化決策,所以部分的机器学习研究是开发容易处理的近似算法。(Wikipedia)
计算机科学家汤姆·米切尔在其著作的Machine Learning一书中定义的机器学习为: well-posed learning problem
A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
——Tom Mitchell,Machine Learning
良好的学习问题 是 以性能量度P进行衡量,如果一个计算机程序在某类任务T上的性能,随着经验E而提升,那么我们称这个计算机程序能从经验E中学习。
要素 三个
-
模型(这里的线性 指的 是对参数 w )
- 线性方法(指的是 w的线性函数):
- 广义线性方法:
其中是 可学习的 非线性基函数 (基函数用于对x进行特征变换) - 非线性方法:例如神经网络
是激活函数(如 ReLU、Sigmoid)这个模型的 非线性来自激活函数和多层结构。
- 线性方法(指的是 w的线性函数):
-
学习准则 (学习目标 优化目标)
-
期望风险:这个是最理论化的目标 指的是 损失值在真实数据分布下的期望,但是由于 数据的真实分布
是不可知的,所以通常难以计算
-
经验风险:根据大数定律 当数据量足够大时 可以用频率当做分布 所以有经验风险
$$
\cal{R}{emp}(f) = \frac{1}{n} \sum{i=1}^{n} L(f(x_i), y_i)
$$ -
结构风险最小化:在结构风险基础上加上正则化项 防止模型过拟合 控制模型的复杂程度
$$
\cal{R}{srm}(f) = R{emp}(f) + \lambda \cdot \Omega(f)
$$
其中是控制正则损失系数 -
最大间隔准则: 在SVM支持向量机中的学习准则
间接最小化结构,优先选更稳健的模型 -
最大似然估计(MLE):最大似然
-
贝叶斯后验最大化(MAP):
加了先验的 MLE 可以当做正则化的MLE
-
-
优化
-
梯度下降方法
方法名 特点 备注 标准梯度下降(GD) 每次用全量样本更新 计算量大,收敛稳定 随机梯度下降(SGD) 每次只用一个样本 噪声大但效率高 小批量梯度下降(Mini-batch GD) 综合GD和SGD优点 深度学习常用 Momentum(动量法) 加速收敛,抗震荡 模拟物理惯性 Nesterov Accelerated Gradient(NAG) 改进动量法 预判未来梯度方向 Adagrad 自适应每个参数学习率 学习率随训练减小,可能太快收敛 RMSProp 改进Adagrad,控制过快下降 常用于RNN Adam 融合Momentum和RMSProp 最常用,鲁棒性好 AdamW 改进了Adam的权重衰减策略 Transformer常用 -
二阶优化方法
方法名 特点 备注 牛顿法(Newton’s Method) 用二阶导数加快收敛 每次迭代代价高 拟牛顿法(如BFGS、L-BFGS) 近似二阶信息 在小数据场景表现好 自然梯度法(Natural Gradient) 考虑参数空间结构 常用于贝叶斯/强化学习 -
无梯度优化
方法名 特点 适用场景 网格搜索 / 随机搜索 超参数调优经典方法 参数少时可用 进化算法(如遗传算法GA) 模拟自然选择过程 黑盒优化 粒子群优化(PSO) 模拟群体智能 连续优化有效 模拟退火(SA) 模拟物理退火过程 全局优化倾向强 贝叶斯优化(BO) 利用代理模型迭代搜索 少样本高效搜索
-
过拟合、欠拟合、正则化
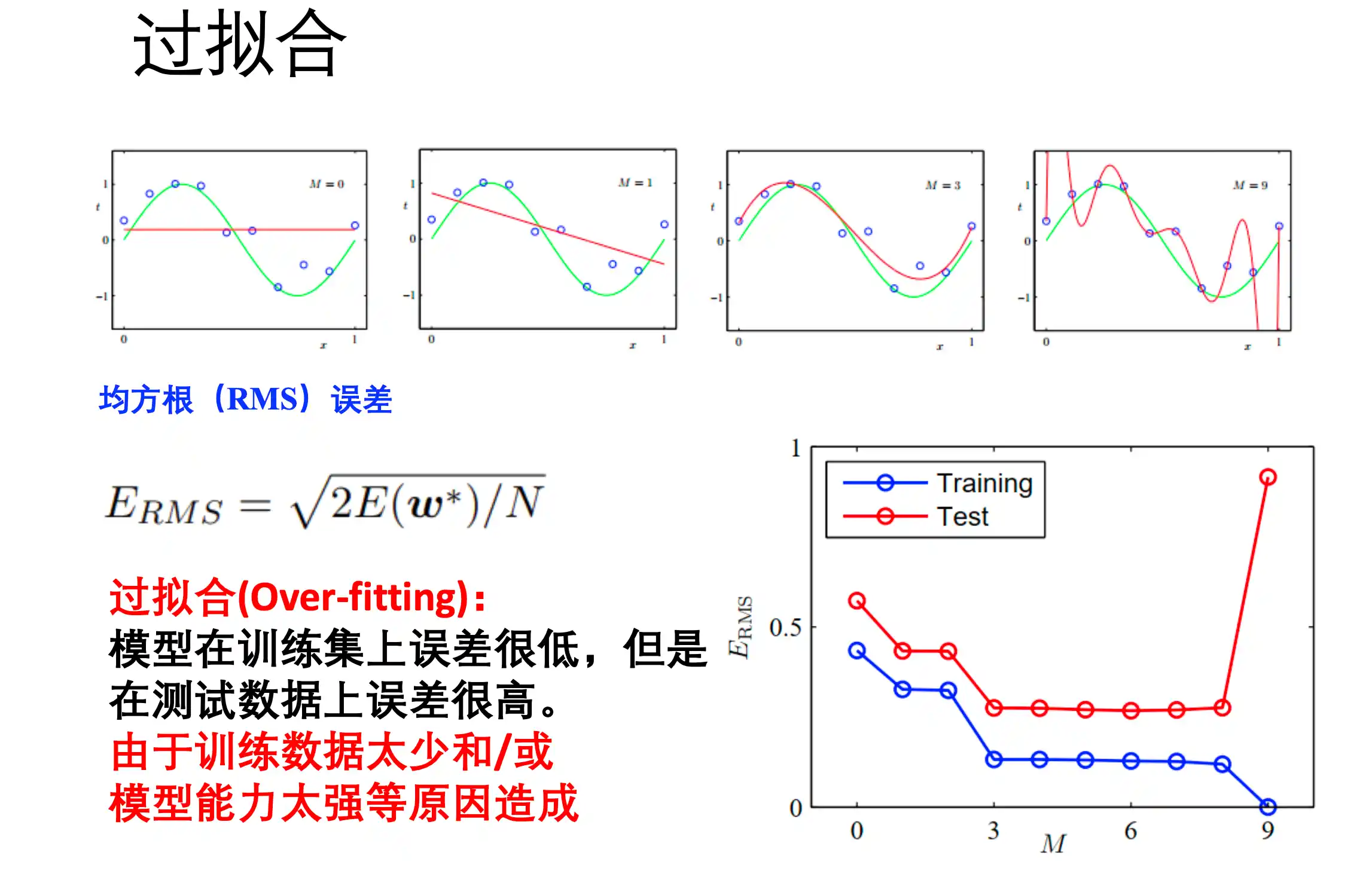
过拟合
过拟合(Over-fitting)是指 模型在训练集上面误差很低,但是在测试机上误差很高。对训练集拟合的能力过强。
过拟合的解决方法:
- 扩大数据集
- 正则化 (奥卡姆剃刀原理 简单有效)
如果没有必要就不要增大模型的数量 - 通过 验证集合 来选择模型
K折交叉验证:训练K次判断模型能力
留一法 K=N
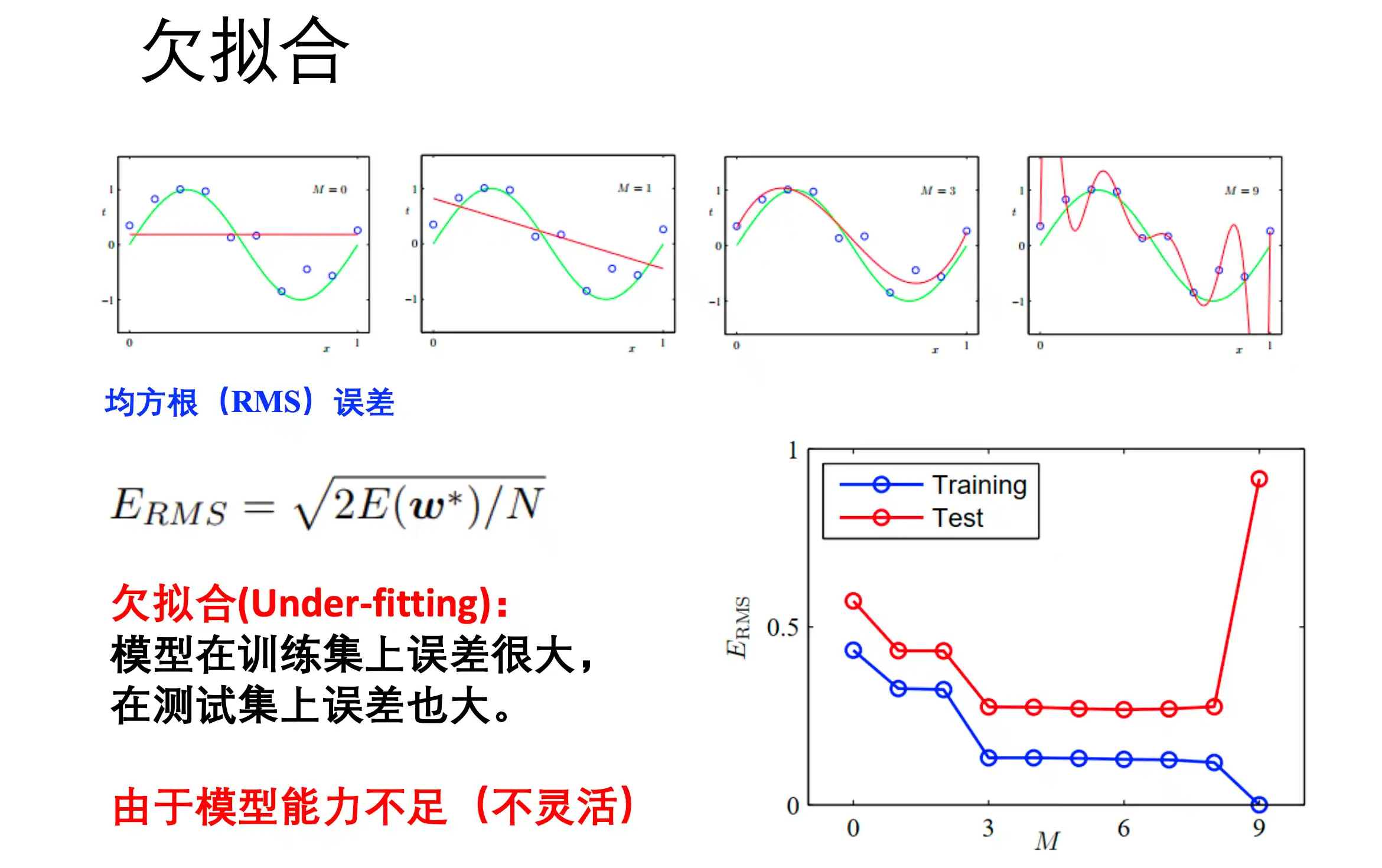
欠拟合
模型在训练集和测试集上的误差都很大。由于模型能力不足(不够灵活)
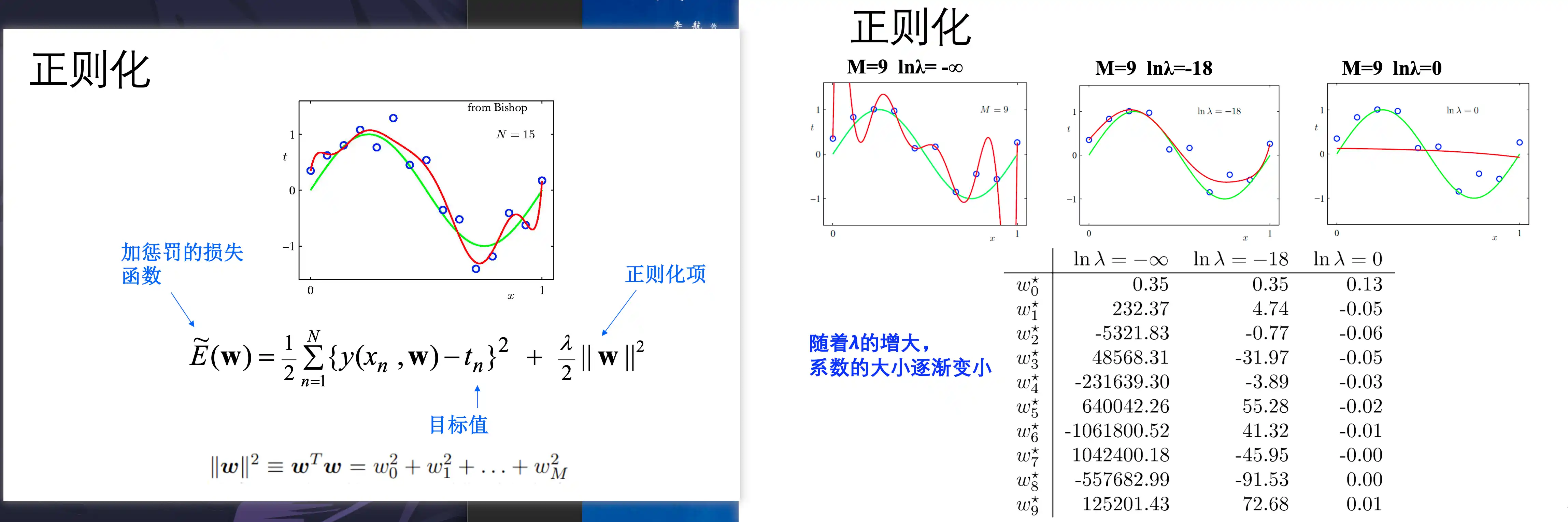
正则化
对模型的损失中 添加正则化损失 例如L1、L2
奥卡姆定律 简单有效
贝叶斯公式
后验 似然x先验
第二章 概率论与优化
概率的概念、贝叶斯学派vs频率轮学派
概率的概念
概率是对不确定事件发生可能性的度量。在数学上,概率是定义在样本空间上的一个函数,取值范围是 [0,1] 。
但不同学派对“概率的意义”有不同理解,主要有:
频率学派(Frequentist)
观点:
概率是一个事件在大量重复试验中出现的相对频率。
通过大量独立实验将概率解释为事件发生频率的均值(大数定律)。
举个例子:如果你连续掷硬币很多次,有一半是正面,那我们就说正面概率是 0.5。
特点:
- 概率是客观的,跟你是否知道某个信息无关。
- 参数是固定未知数,不能被建模成随机变量。
- 推断方法:最大似然估计(MLE)、假设检验、置信区间等。
贝叶斯学派(Bayesian)
观点:
概率是表示一个人对事件发生的主观相信程度,是对不确定性的度量。
将概率解释为信念度(degree ofbelief)。当考虑的试验次数非常少的时候,贝叶斯方法的解释非常有用。此外,贝叶斯理论将我们对于随机过程的先验知识纳入考虑,当我们获得新数据的时候,这个先验的概率分布就会被更新到后验分布中。
举个例子:如果你知道这枚硬币偏向正面,你就可以给出“正面概率0.8”,即使你还没开始掷。
特点:
- 概率可以用于表示对未知参数的信念。
- 参数也可以是随机变量。
- 推断方法:利用贝叶斯公式更新先验分布得到后验分布。
两者对比总结:
| 内容 | 频率学派 | 贝叶斯学派 |
|---|---|---|
| 概率定义 | 事件长时间频率 | 主观信念 |
| 参数看法 | 固定未知值 | 随机变量 |
| 推断结果 | 单个估计值 | 概率分布 |
| 常用方法 | MLE、假设检验 | 贝叶斯公式、先验-后验推断 |
伯努利分布、高斯分布
伯努利分布 Bernouli
就是 单次的 二项分布 :
期望
二项分布:
期望
共轭性:
高斯分布
就是正态分布:
期望
极大似然估计、最大后验估计
极大似然估计 和 最大后验估计 都是 机器学习三要素中的 学习准则
极大似然估计(Maximum Likelihood Estimate)MLE
选择让 观测到数据出现的概率最大的 一组参数 , 下面这个P就是似然函数
最大后验估计 (Maximum A Posteriori estimate)MAP
在给定 先验参数分布 和 数据
梯度下降以及不同形式
Goal:
Just iterate
where

| 方法名 | 特点 | 备注 |
|---|---|---|
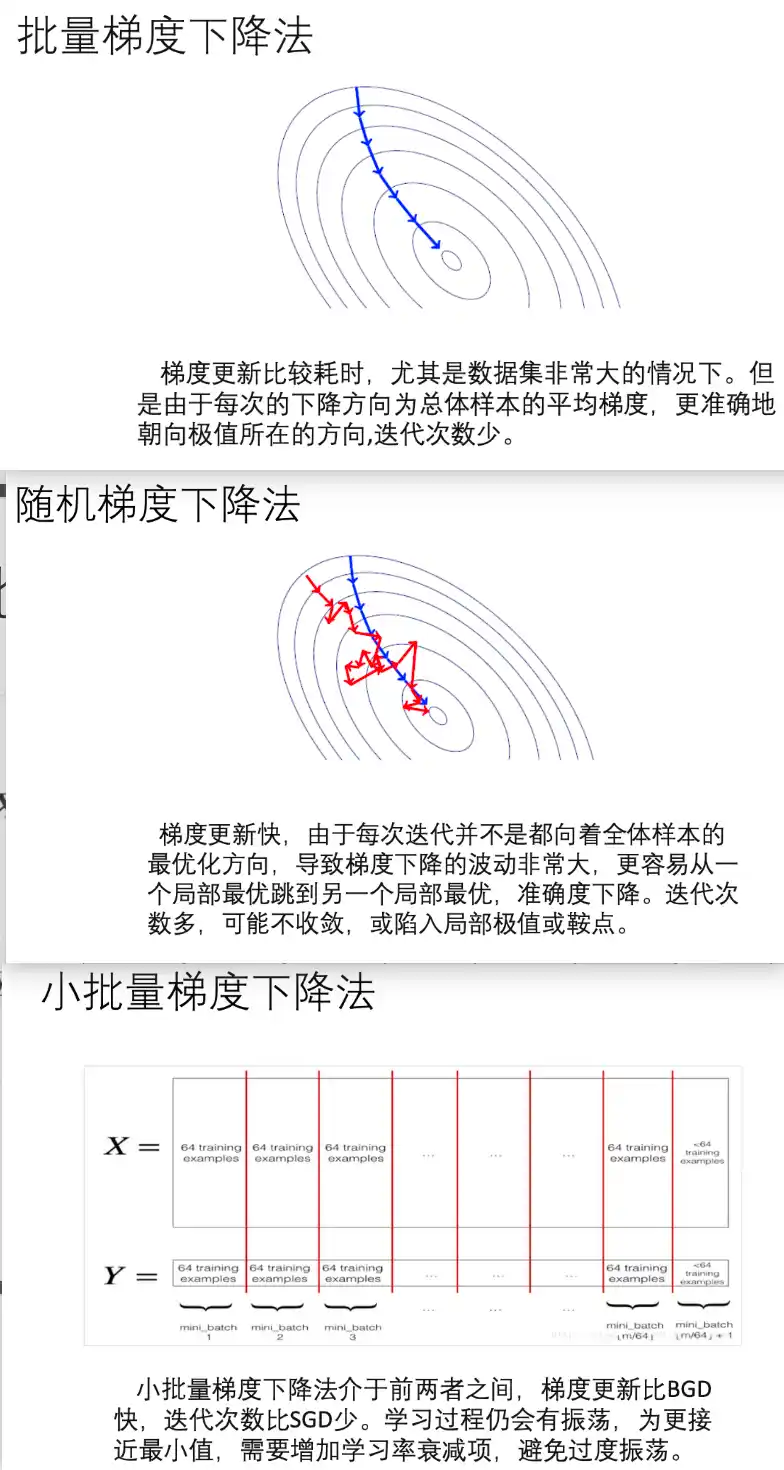
| 标准梯度下降(GD) | 每次用全量样本更新 | 计算量大,收敛稳定。也叫批量梯度下降法BGD |
| 随机梯度下降(SGD) | 每次只用一个样本 | 噪声大但效率高 |
| 小批量梯度下降(Mini-batch GD) | 综合GD和SGD优点 | 深度学习常用 |
| Momentum(动量法) | 加速收敛,抗震荡 | 模拟物理惯性 |
| Nesterov Accelerated Gradient(NAG) | 改进动量法 | 预判未来梯度方向 |
| Adagrad | 自适应每个参数学习率 | 学习率随训练减小,可能太快收敛 |
| RMSProp | 改进Adagrad,控制过快下降 | 常用于RNN |
| Adam | 融合Momentum和RMSProp | 最常用,鲁棒性好 |
| AdamW | 改进了Adam的权重衰减策略 | Transformer常用 |
 |
||
 |
||
 |
第三章 回归的线性模型
介绍
什么是回归? 回归指的是 让模型 预测连续的数值型输出(即实数范围内的值)
什么是线性模型? 线性模型指的是 模型 是 参数w 的线性函数 一般形式为
向量形式为
其中
线性模型的优点:简单易建模 可解释性强 非线性模型(引入层级结构或者高位映射)的基础 。
线性回归是什么?
给定数据集
线性回归的目的 学到一个线性模型 尽可能 准确地 预测 实值输出
线性回归最小二乘法
建立线性模型 为了方便 表达 把 b 和 1 增广入 w x 中




多元线性回归



基函数


基函数 可以选择
- 多项式基函数[
] - 高斯基函数 [
] - sigmoid 基函数[
]
岭回归 Ridge Regression 山脊回归
岭回归就是在原本的loss上加上了 权重产生的 权重衰减正则化项


最大化后验概率 等价于 最小化正则化的平方和误差函数

闭式解与几何解释

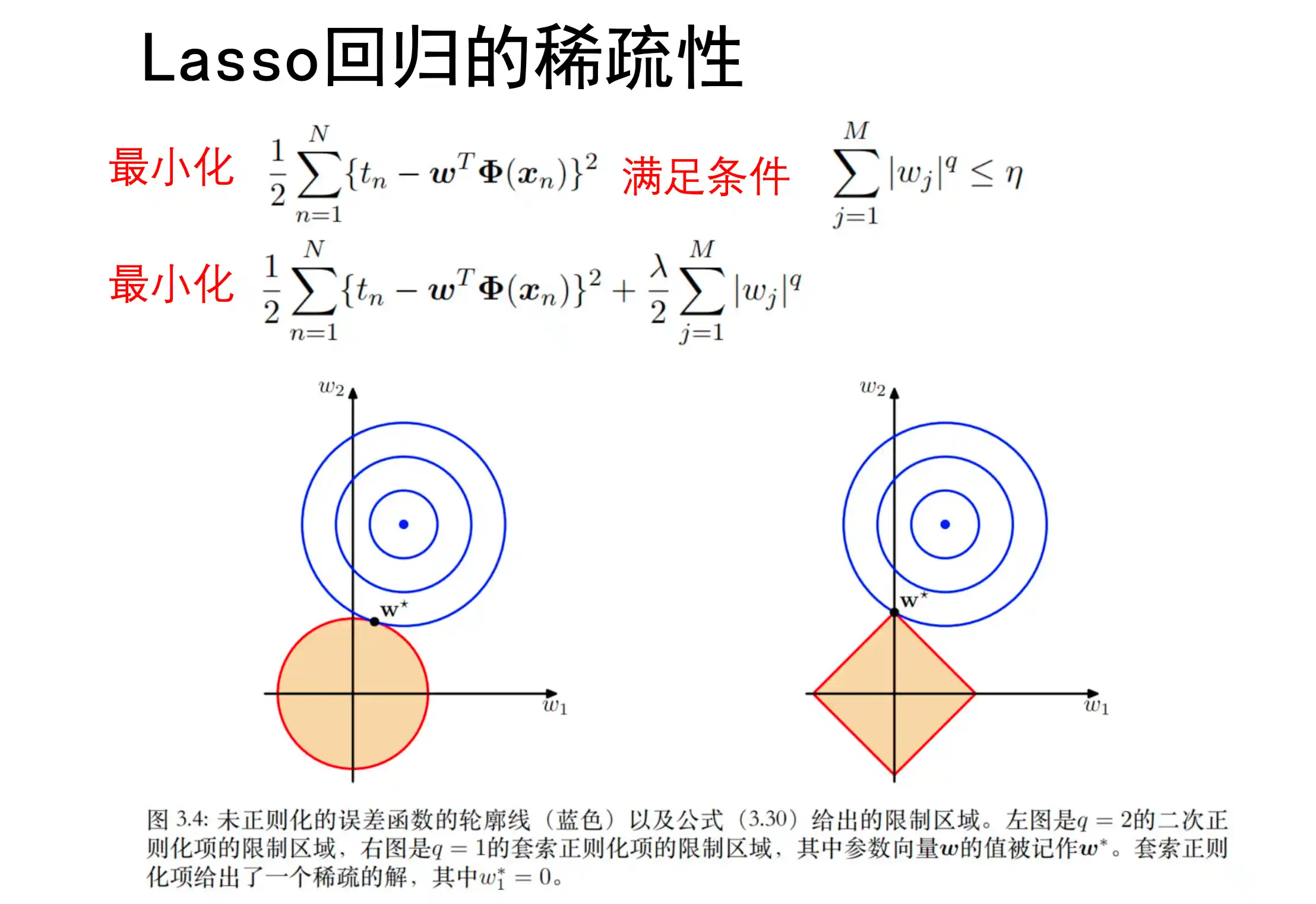
Lasso 回归 套索回归
L1 loss

Lasso回归能够使模型 具有稀疏性
第四章 基础的分类方法
回归是多个输入特征被映射到一个或者多个连续的目标变量
分类则是 输入特征x被映射到K个离散类别之一
线性分类概念
线性分类,模型指的是 分类面 是 x 的 线性 函数 (分类函数 f 可能是非线性函数 例如在外面加了一层 sigmoid)
区别于前面的线性回归(对于参数是线性的)
推广的线性模型 用非线性函数对w的线性函数的结果进行激活


下面说的三种 感知机 logistic回归 朴素贝叶斯分类器
感知机和logistic回归两种是严格线性的 决策面是超平面
朴素贝叶斯分类器 通常是非线性 其决策边界取决于特征的条件概率分布(如高斯朴素贝叶斯的决策边界是二次曲面)
若特征的条件概率分布属于指数族(如泊松分布),且满足特定条件时,可能得到线性决策边界。
三种类型:判别函数、概率生成模型、概率判别模型
判别函数 Discriminant Function (感知器)
这个是直接说出结果是哪个 下面的会给出概率 然后再决策是哪个
直接找到一个函数
线性判别函数就是指 决策面 是 超 平面 的判别函数
二分类情形
线性判别函数 y=0 就是 决策平面

几何性质 【2|1】
如过用一个二分类器 处理多分类的情况,可以:
- 一对其他 分类器(K-1个二分类器)
- 一对一 分类器 (
个二分类器)
但是会出现不可分的区域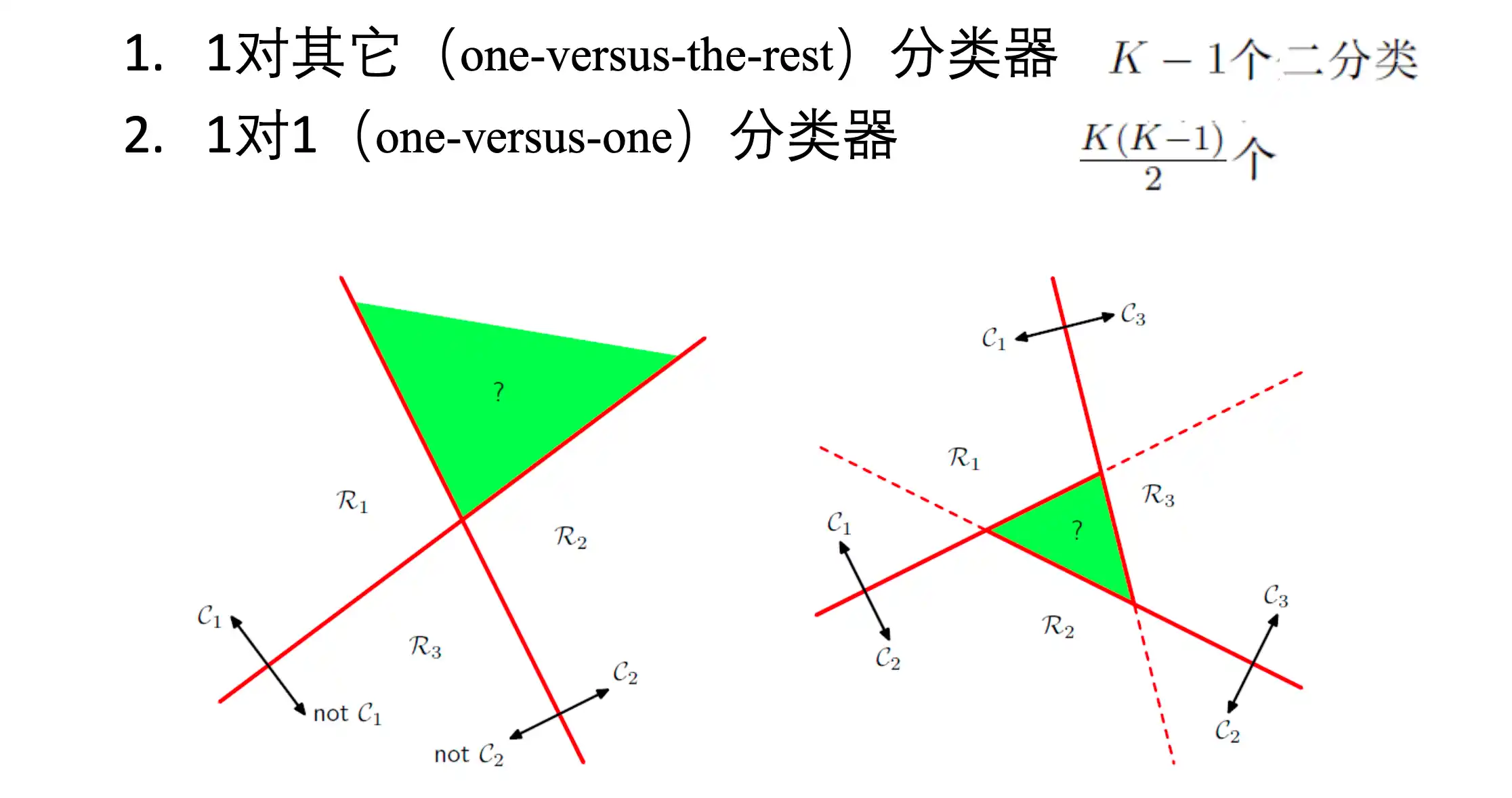
多分类情形
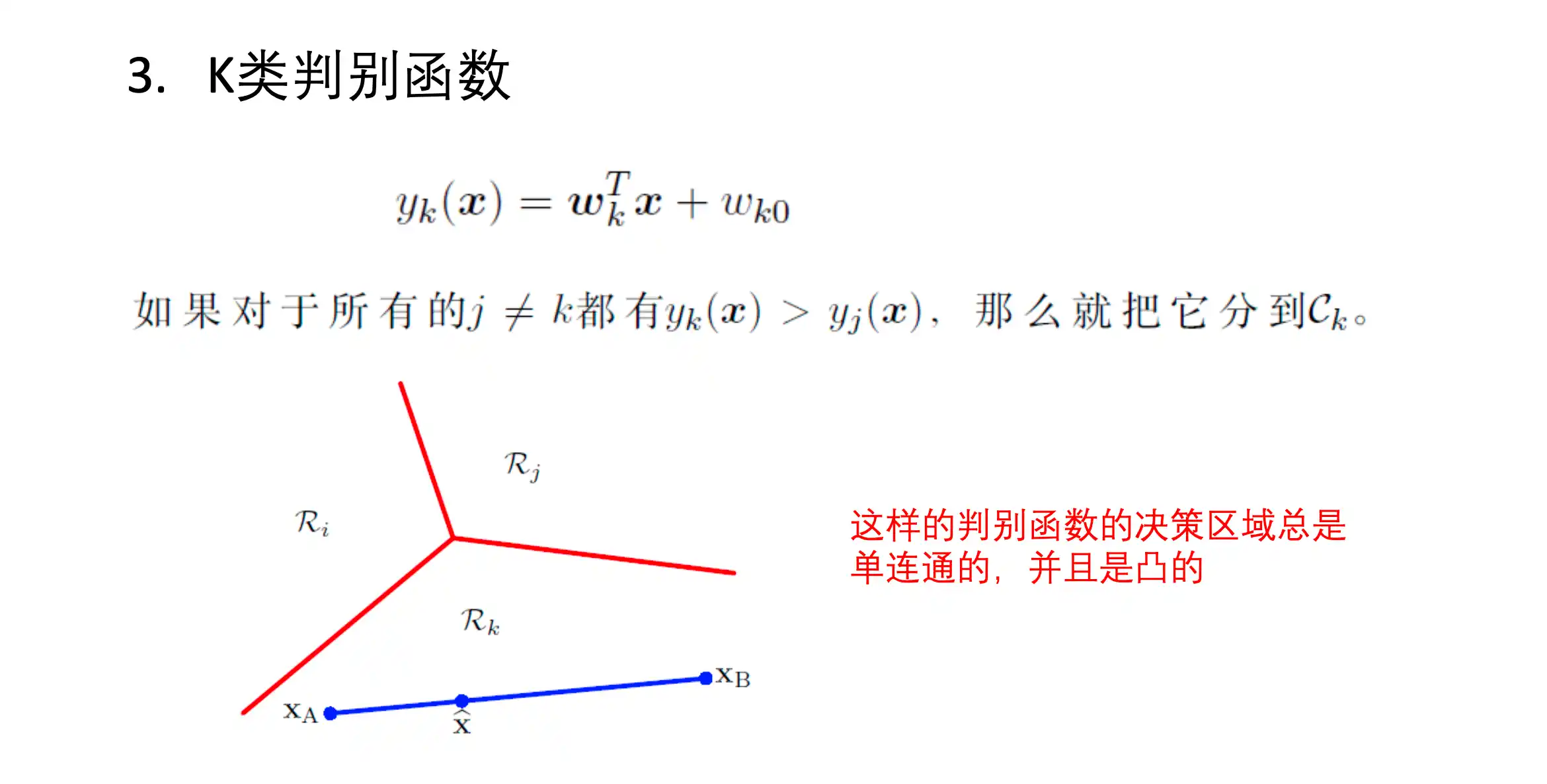
K类判别函数
概率判别模型 Probabilistic Discriminative Models (logistic回归*)
直接对 后验概率
Logistic回归 (分类模型)
在线性模型的基础上 加上了激活函数 得到概率大小 下面的例子用的是sigmoid函数


直接对y=1 对线性函数激活得到概率
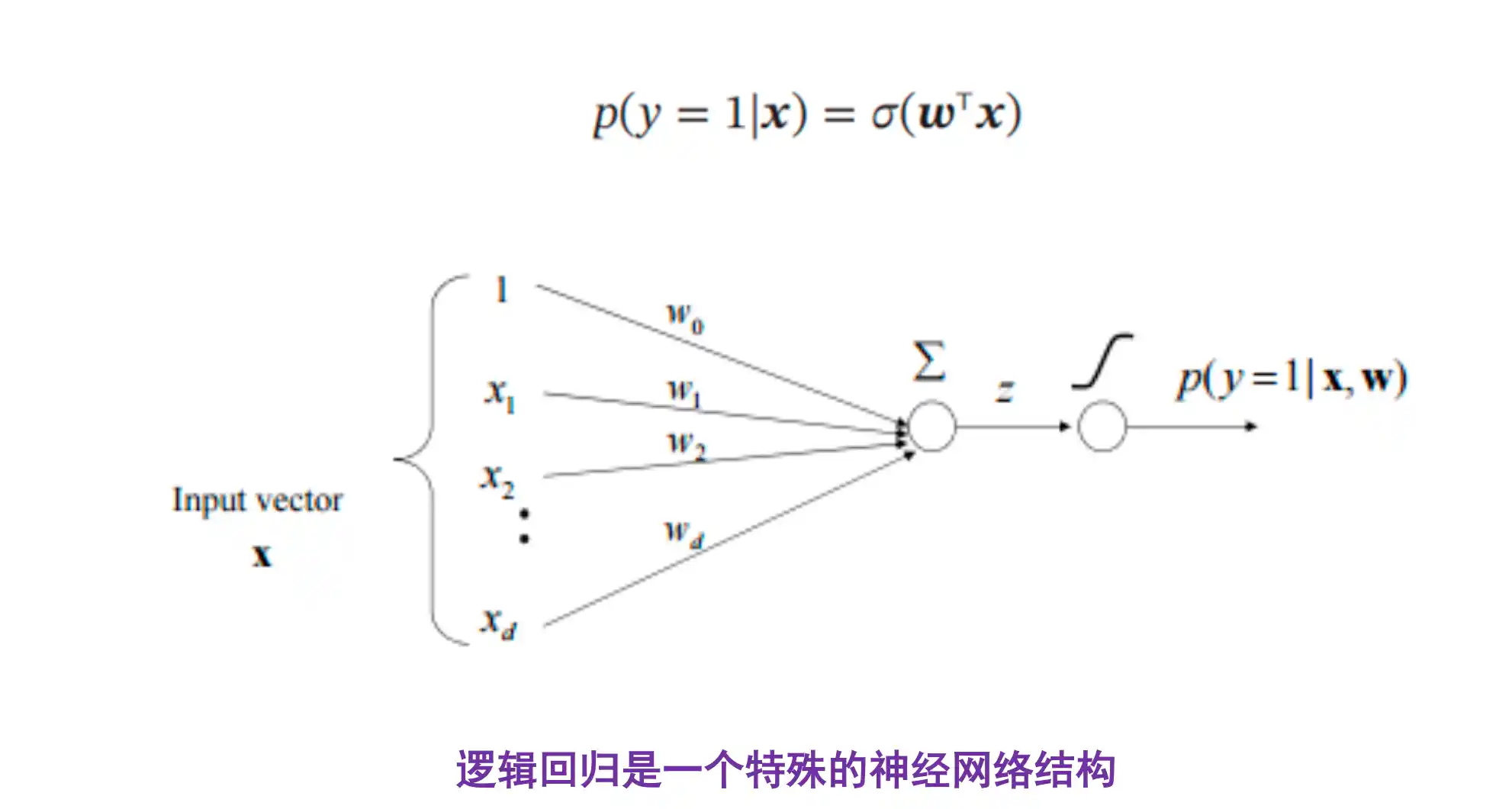
决策面就是两个类别的后验概率相等 也就是 
sigmoid: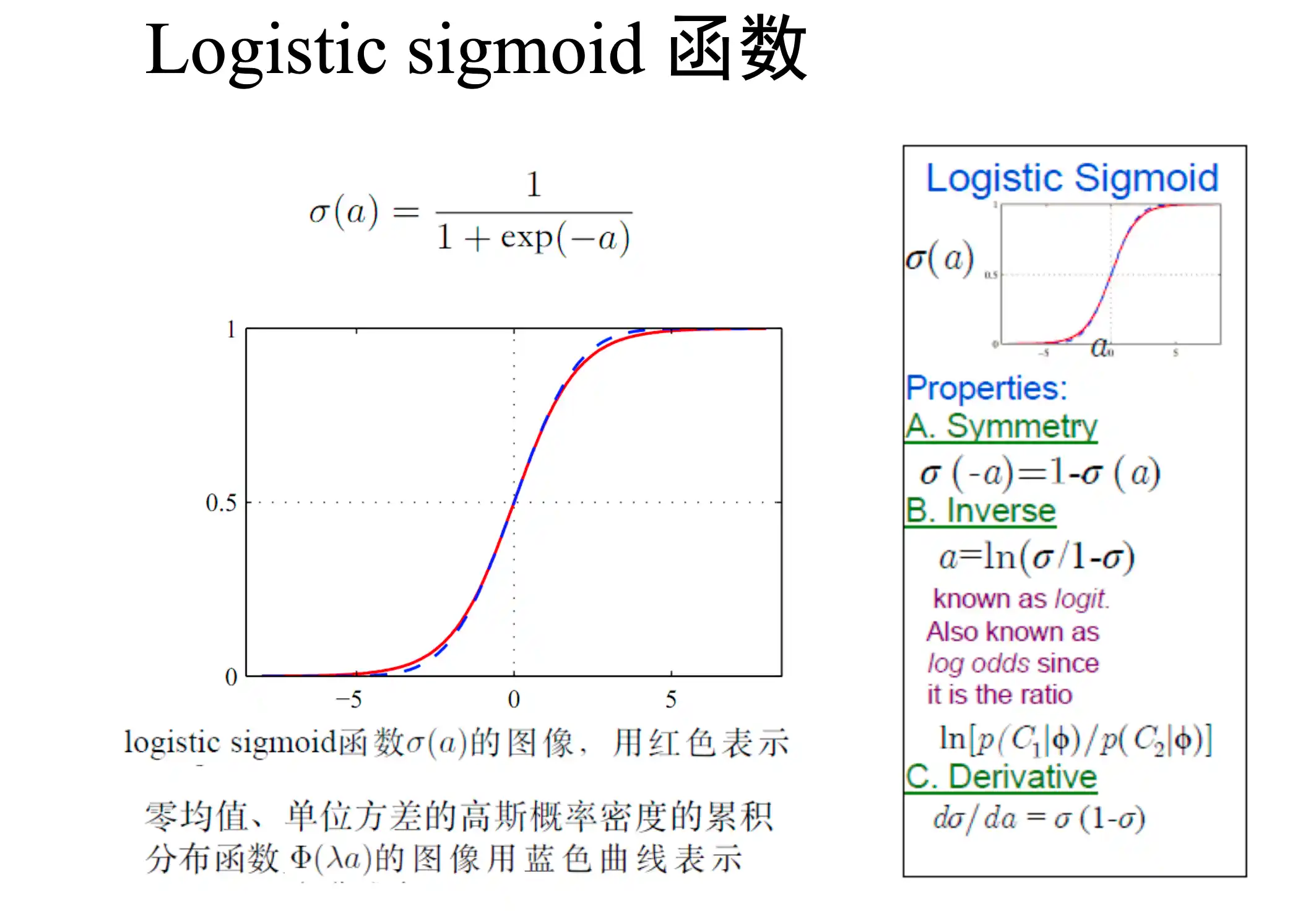
逻辑回归模型的训练



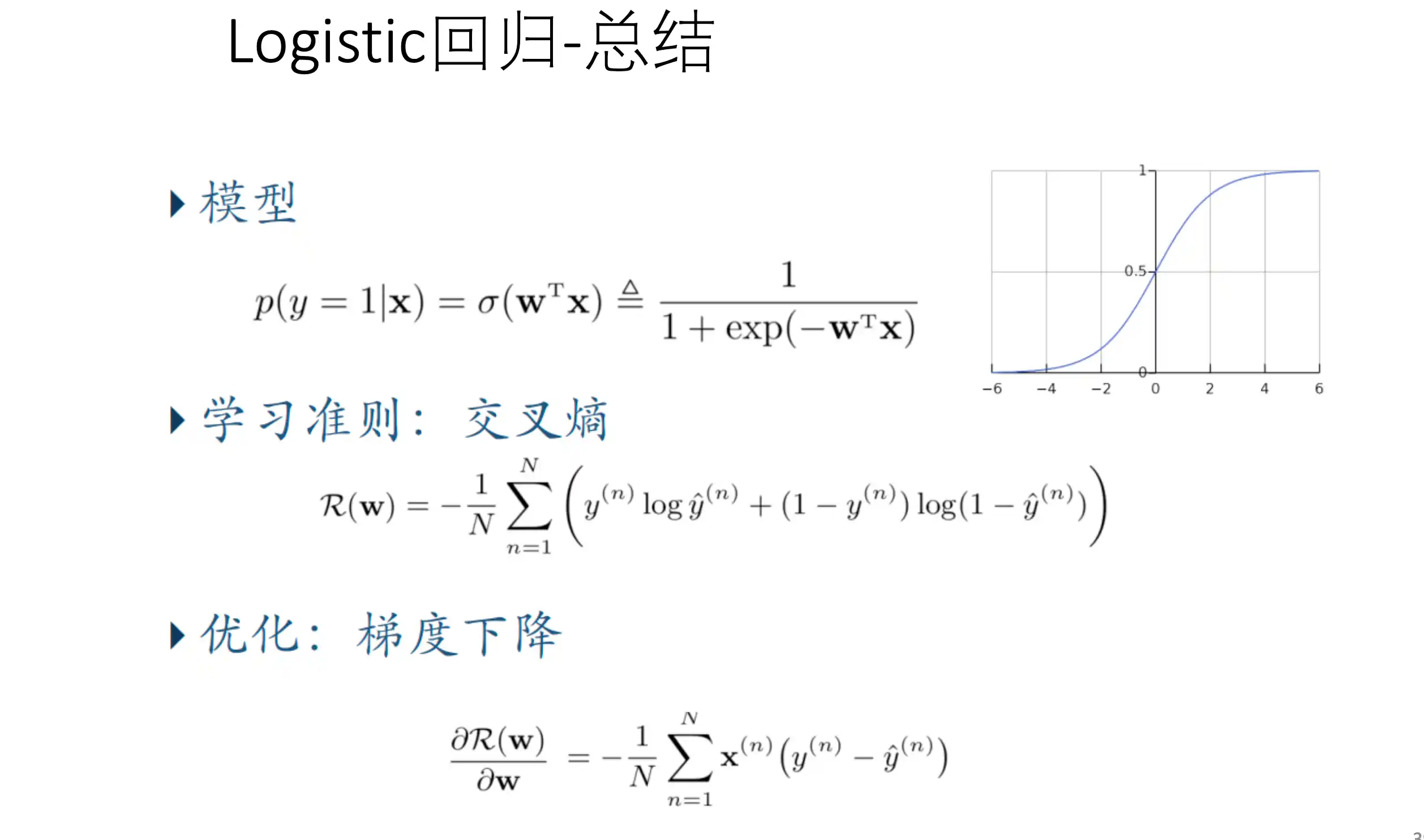
逻辑回归就是在线性回归模型的基础上套了一个sigmoid LOSS就是两个类别的的交叉熵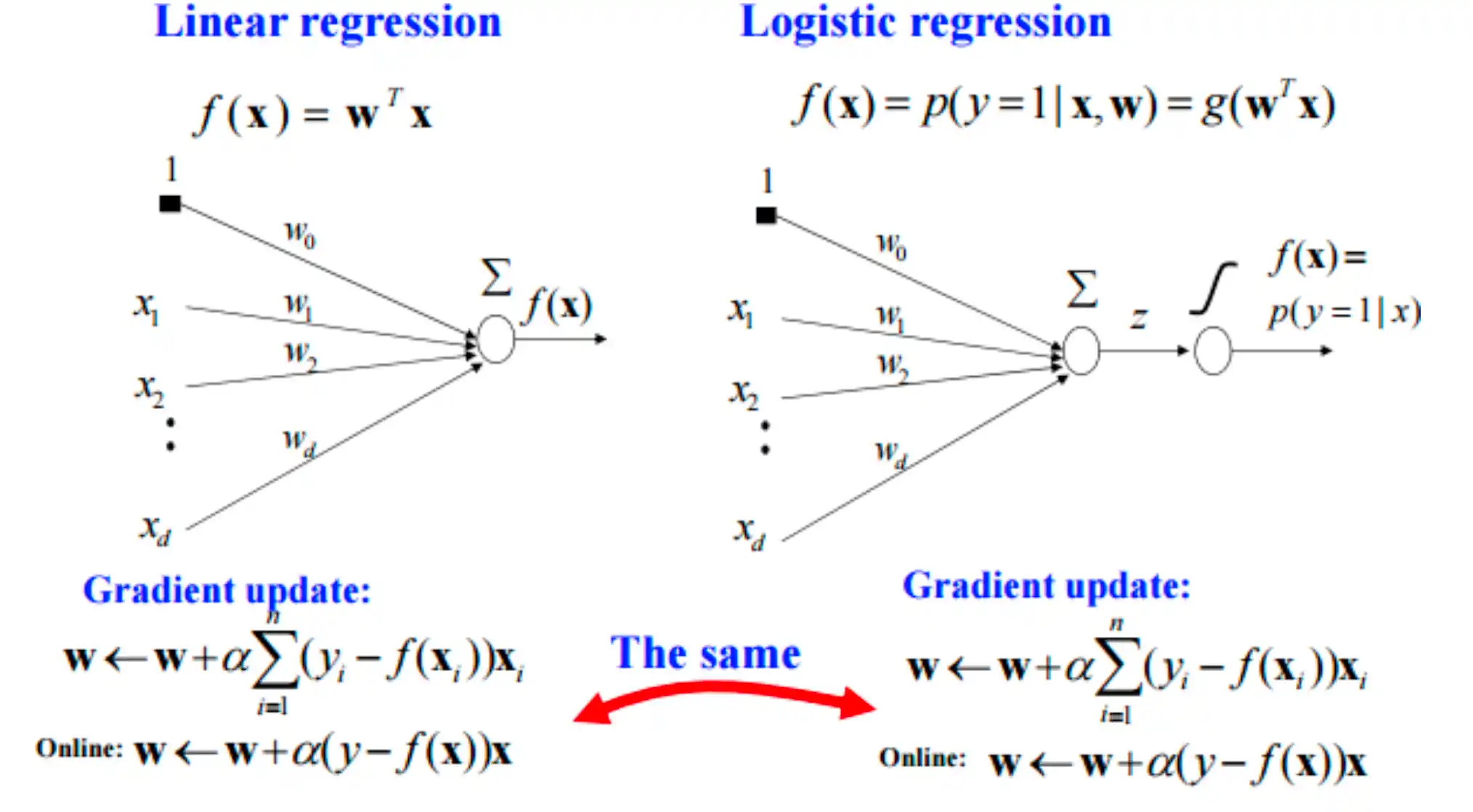
逻辑回归和神经网络模型的对比
| 特性 | 逻辑回归 | 神经网络 |
|---|---|---|
| 模型结构 | 单层(仅输入层 + 输出层) | 多层(输入层 + 隐藏层 + 输出层) |
| 决策边界 | 线性(超平面) | 非线性(可拟合复杂边界) |
| 表达能力 | 只能解决线性可分问题 | 可逼近任意复杂函数(通用近似定理) |
| 参数优化 | 使用梯度下降法优化权重 ( w ) | 使用反向传播(Backpropagation)优化多层权重 |
| 输出类型 | 概率(通过Sigmoid函数) | 概率(Softmax)或任意值(取决于输出层设计) |
| 适用任务 | 二分类(默认)、可扩展至多分类(One-vs-Rest) | 二分类、多分类、回归、生成任务等 |
| 计算复杂度 | 低(参数少,训练快) | 高(参数多,需大量数据和计算资源) |
| 可解释性 | 高(权重直接反映特征重要性) | 低(黑箱模型,难以解释隐藏层) |
概率生成模型 Probabilistic Generative Models (朴素贝叶斯分类器*)
先对 类的条件密度
最后,使用决策论来确定每个输入x的类别
等价地,直接对 联合概率分布
统计类别分布 得到先验 在类内 统计属性分布 得到似然
朴素贝叶斯分类器
估计后验概率的主要困难在于:类条件概率是 x 在所有属性上的联合概率(输入的x有很多维度), 难以用有先限的训练样本估计获得
朴素贝叶斯分类器 采用 属性条件独立性假设 , 每个属性独立地对分类结果发生影响。
更具上述假设 后验概率可以写为(d是属性个数 i是第i个属性):
对于所有类别 P(x) 相同 , 所以贝叶斯判定准则为:
即对每个样本x 选择后验概率最大的类
朴素贝叶斯分类器计算例子

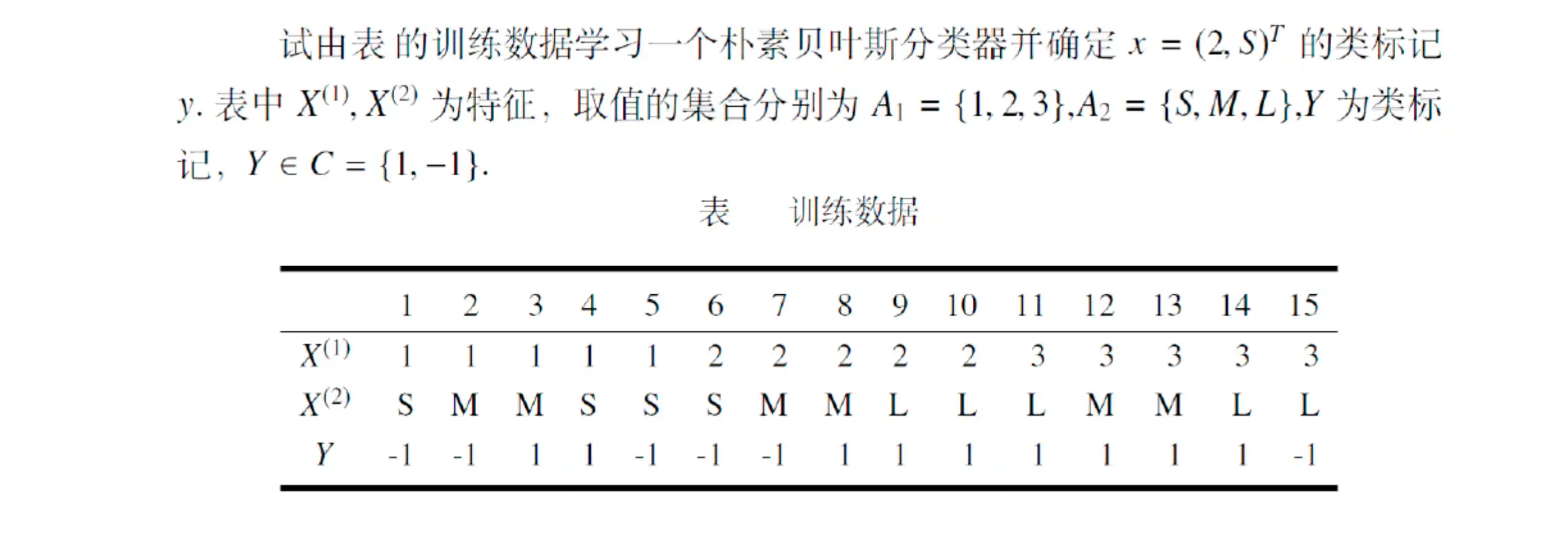

第五章 支持向量机 与 核方法
SVM原理
支持向量机的三个关键想法:
- 通过优化来求解一个超平面分类器
- 寻找最大间隔分类器来提高模型的泛化能力(结构化风险最小)
- 采用 核技巧 使得在高维度特征空间的计算更有效率
假设数据是线性可分的,那么一定存在两条平行的直线分别经过两类样本最外侧的数据 设这两条直线是
在这个设置下 相当于学习一个基于间隔的分类器

为什么要写成
?
主要是为了简化下面的计算,如果写成在计算梯度时候会出现
对偶问题
在解决这个问题时候 使用 拉格朗日乘子法 将其转化为对偶问题:
-
引入拉格朗日乘子
得到拉格朗日函数
-
令
对 和 的偏导数为0可得:
-
回代:
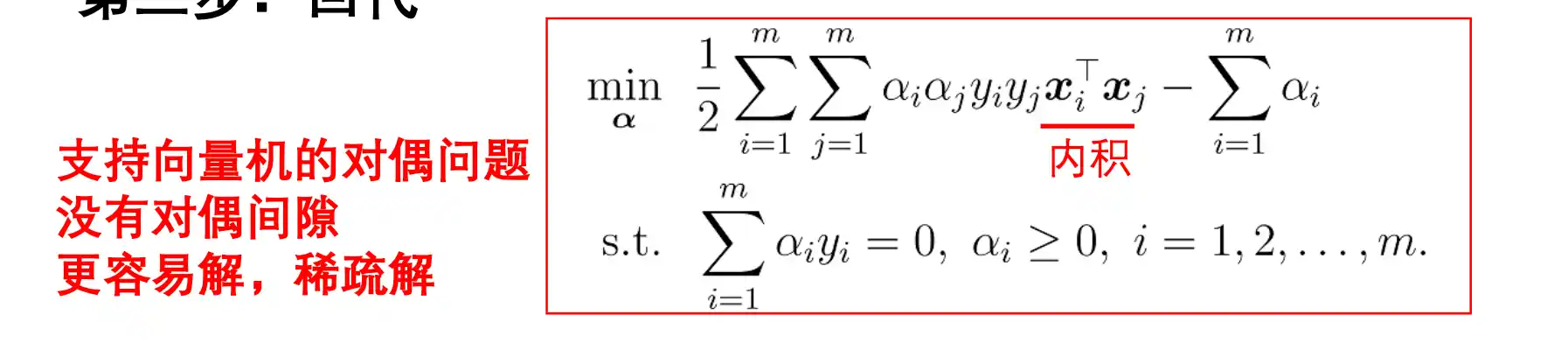
拉格朗日乘子法:通过乘子将约束引入函数得到一个无约束的函数
支持向量就是 wx+b=±1 的向量 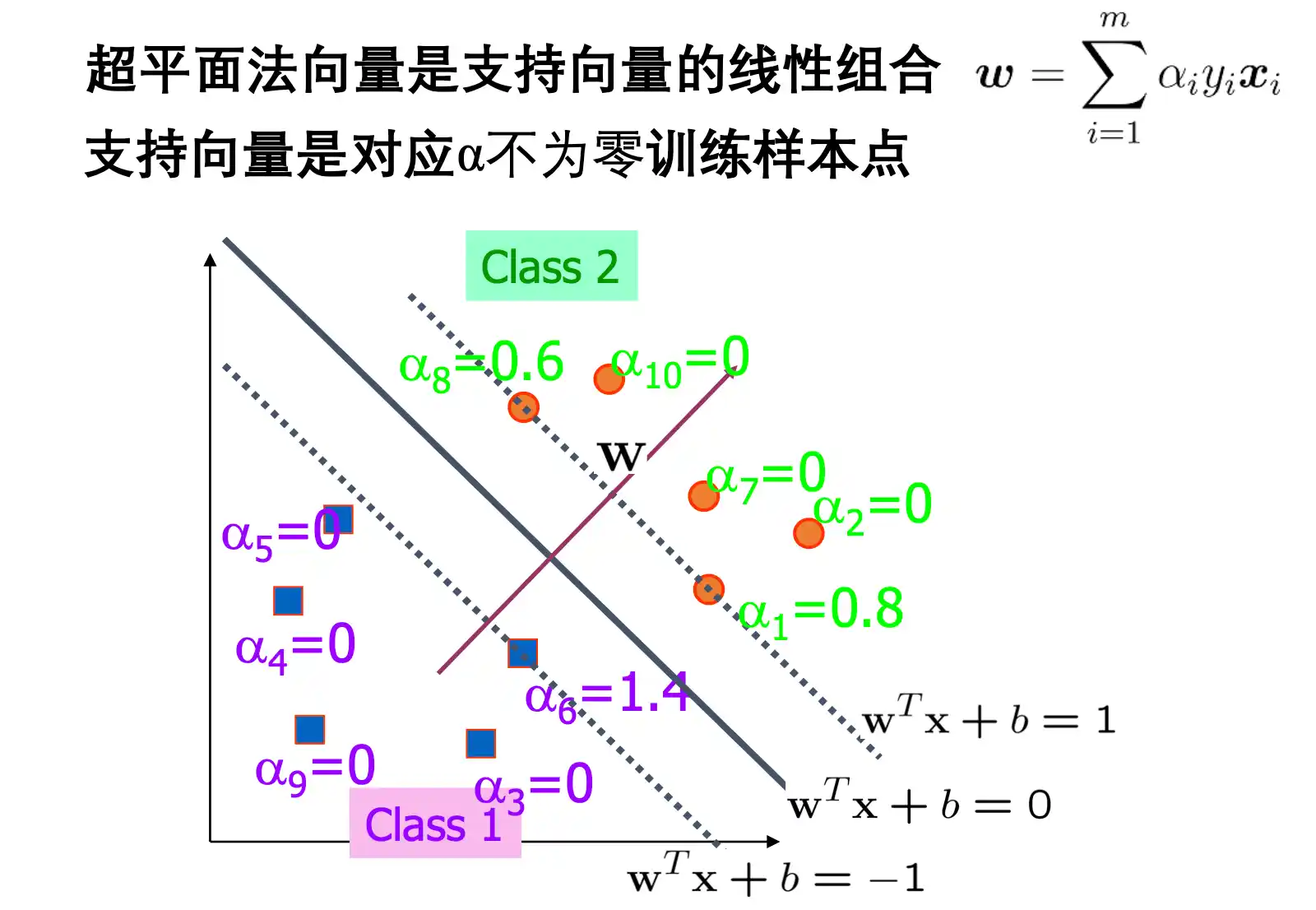
核技巧
一般的 上面所提到的支持向量机是对于 数据线性可分 的情况 , 但是可能存在线性不可分的数据,这样就要把 x 变换到高维空间 使其在高维空间中线性可分。
设样本 x 映射后的向量为

也就是说 两个x的高维表示 都是内积的形式存在 不用显式的计算出来 所以引入 核函数 来代替:
核函数的优点:不需要知道和计算
存在判定
常用核函数
实现非线性分类
通过这个解出后 可以得到 决策函数 $f(x)=sgn(\sum^l_{i=1}y_i\alpha^K(x_i,x)+b^)$
第六章 集成学习
集成学习的概念和类型
集成学习 是通过 构建并结合多个学习器来完成学习任务,提升性能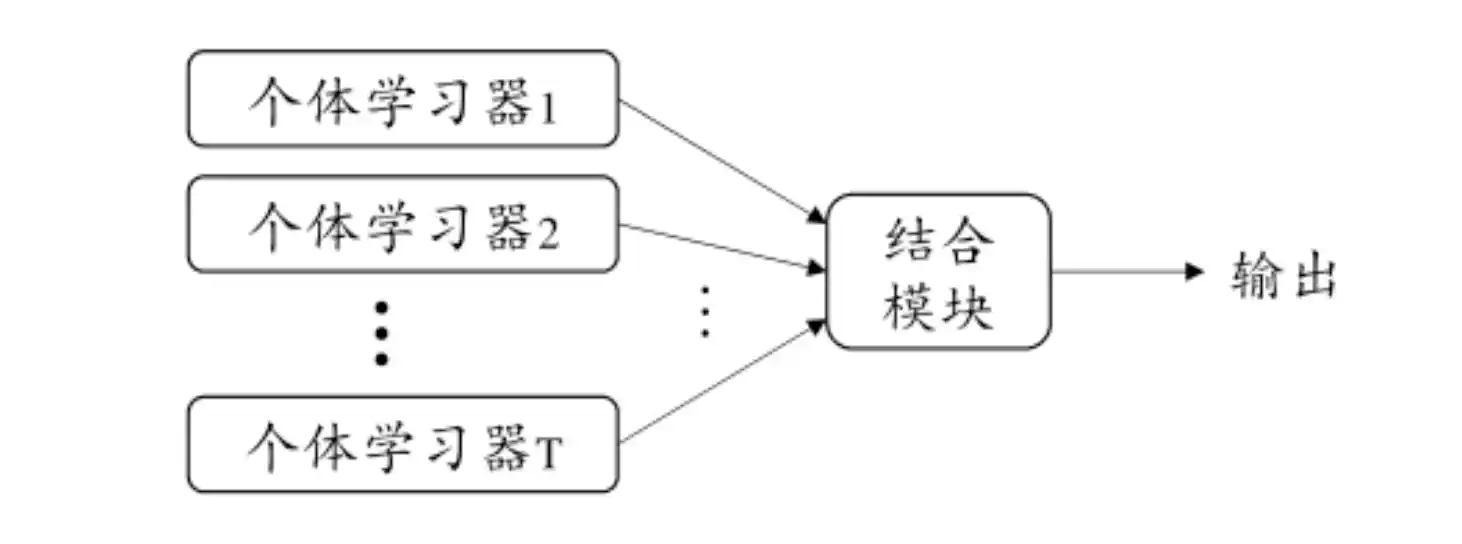
学习器可以是 同质的 也可以是 异质的 (个体学习器由不同的学习算法生成 成为 组件学习期)
其中的同质 个体学习器 称为 基学习器 对应的算法叫做 基学习算法
弱学习器:精度略高于随机 强学习器:精度较高


简单分析
然而我们必须注意到,上面的分析有一个关键假设:基学习器的误差相互 独立.在现实任务中,个体学习器是为解决同一个问题训练出来的,它们显然不 可能相互独立!事实上,个体学习器的“准确性”和“多样性”本身就存在冲 突.一般的,准确性很高之后,要增加多样性就需牺牲准确性,事实上,如何产 生并结合“好而不同”的个体学习器,恰是集成学习研究的核心.
根据个体学习器的生成方式,目前的集成学习方法大致可分为两大类,即 个体学习器间存在强依赖关系、必须串行生成的序列化方法,以及个体学习器 间不存在强依赖关系、可同时生成的并行化方法;前者的代表是Boosting,后 者的代表是 Bagging 和“随机森林”(Random Forest).
AdaBoost算法流程








这个

例子




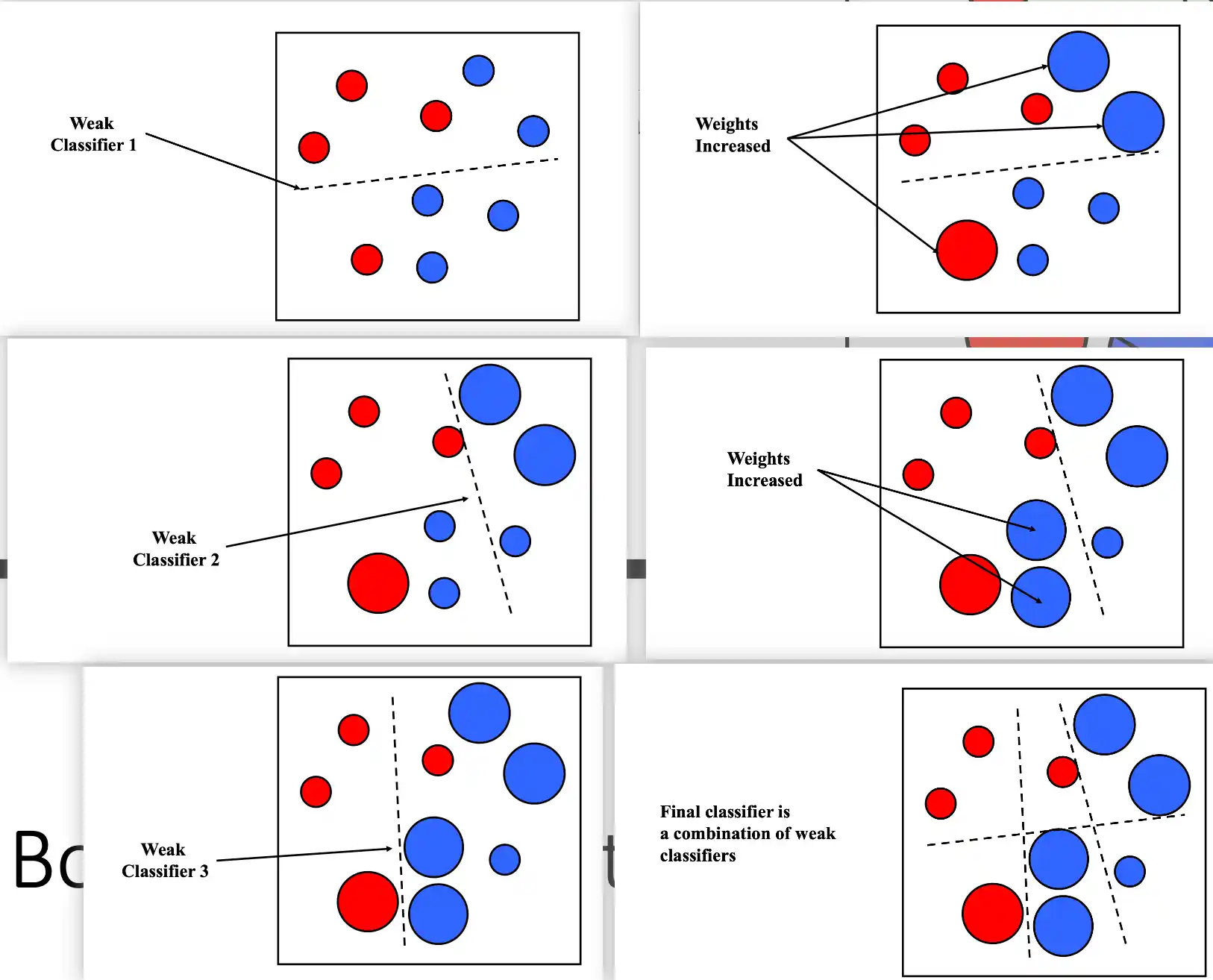
Bagging算法流程
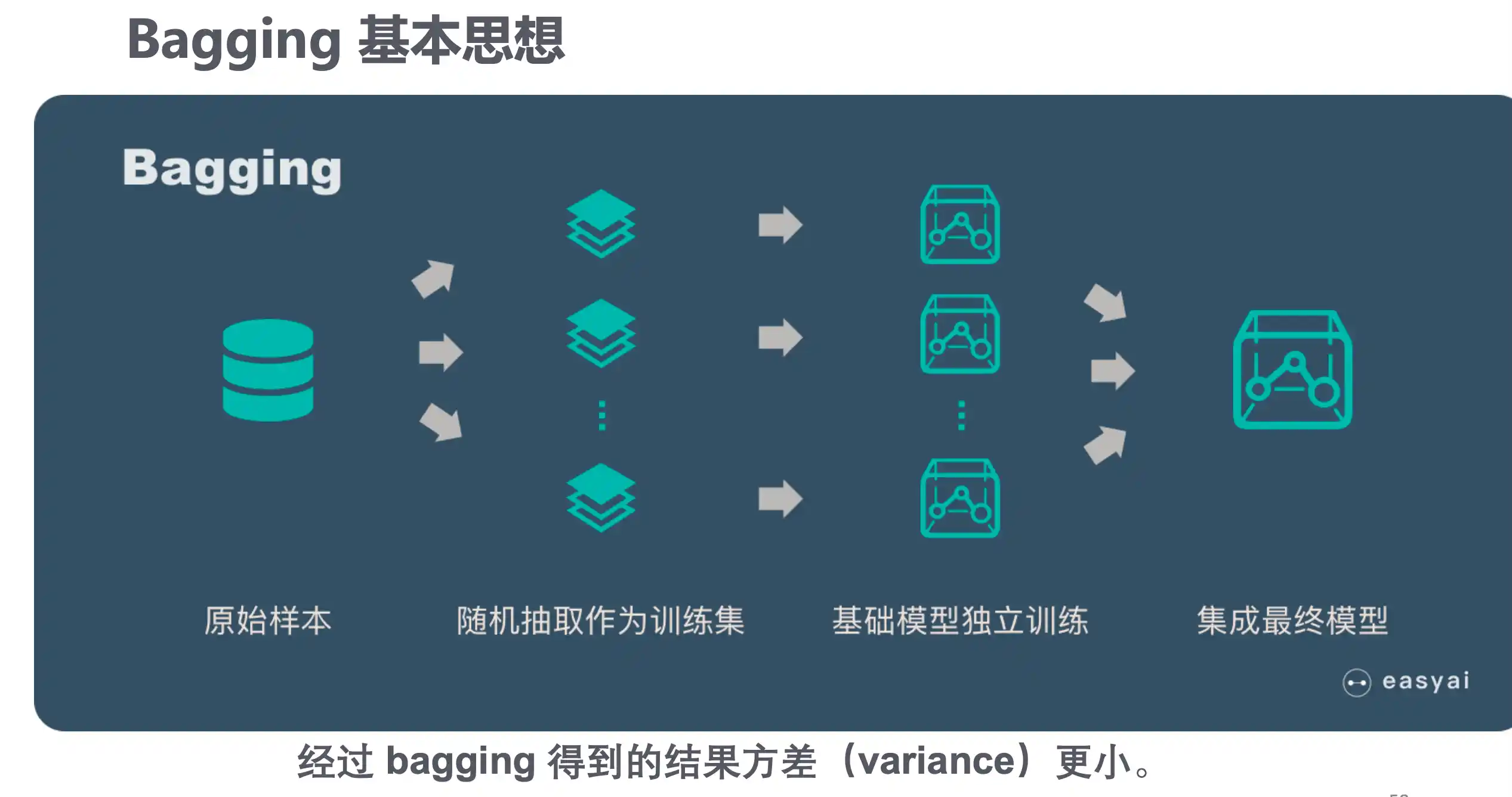
欲得到泛化性能强的集成,集成中的个体学习器应尽可能相 互独立;虽然“独立”在现实任务中无法做到,但可以设法使基学习器尽可能 具有较大的差异.给定一个训练数据集,一种可能的做法是对训练样本进行采 样,产生出若干个不同的子集,再从每个数据子集中训练出一个基学习器.这 样,由于训练数据不同,我们获得的基学习器可望具有比较大的差异.然而,为 获得好的集成,我们同时还希望个体学习器不能太差.如果采样出的每个子集 都完全不同,则每个基学习器只用到了一小部分训练数据,甚至不足以进行有 效学习,这显然无法确保产生出比较好的基学习器.为解决这个问题,我们可考 虑使用相互有交叠的采样子集.

大I 是指数函数 在里面为真假时取1,0
对预测输出进行结合时,通常对分类任务使用简单投票法,对于回归问题使用简单平均法。

获取每个基学习器的训练集方法
包外估计 用 训练集 不包括x的对x做预测
第七章 聚类方法
无监督学习
是机器学习的一种范式,其核心特点是模型从未标注的数据中自动发现隐藏的模式、结构或规律,而无需人工提供标签(即没有明确的“正确答案”作为监督信号)。与监督学习不同,无监督学习的目标是探索数据本身的内在特性。
- 模型: 函数, 条件概率分布 或者条件概率分布
- 策略:目标函数优化
- 算法: 迭代算法,通过迭代达到对目标函数的最优化
聚类
是将样本集合中相似的样本(实例)分配到相同的类,不相似的样本分配到不同的类。 聚类时,样本通常是欧氏空间中的向量,类别不是事先给定,而 是从数据中自动发现,但类别的个数通常是事先给定的。样本之间的相似度或距离由应用决定。 ·如果一个样本只能属于一个类,则称为硬聚类(hard clustering),如果一个样本可以属于多个类,则称软聚类(soft clustering)。
聚类算法有 原型(k均值、高斯混合模型)、密度、层次、谱聚类
K均值算法流程以及特点
K均值聚类是基于样本集合划分的聚类算法。将样本集合划分为k个子集,构成k个类,将n个样本分到k个类别中,每个样本到其所属类的中心距离最小。硬聚类算法,每个样本只有一个类。

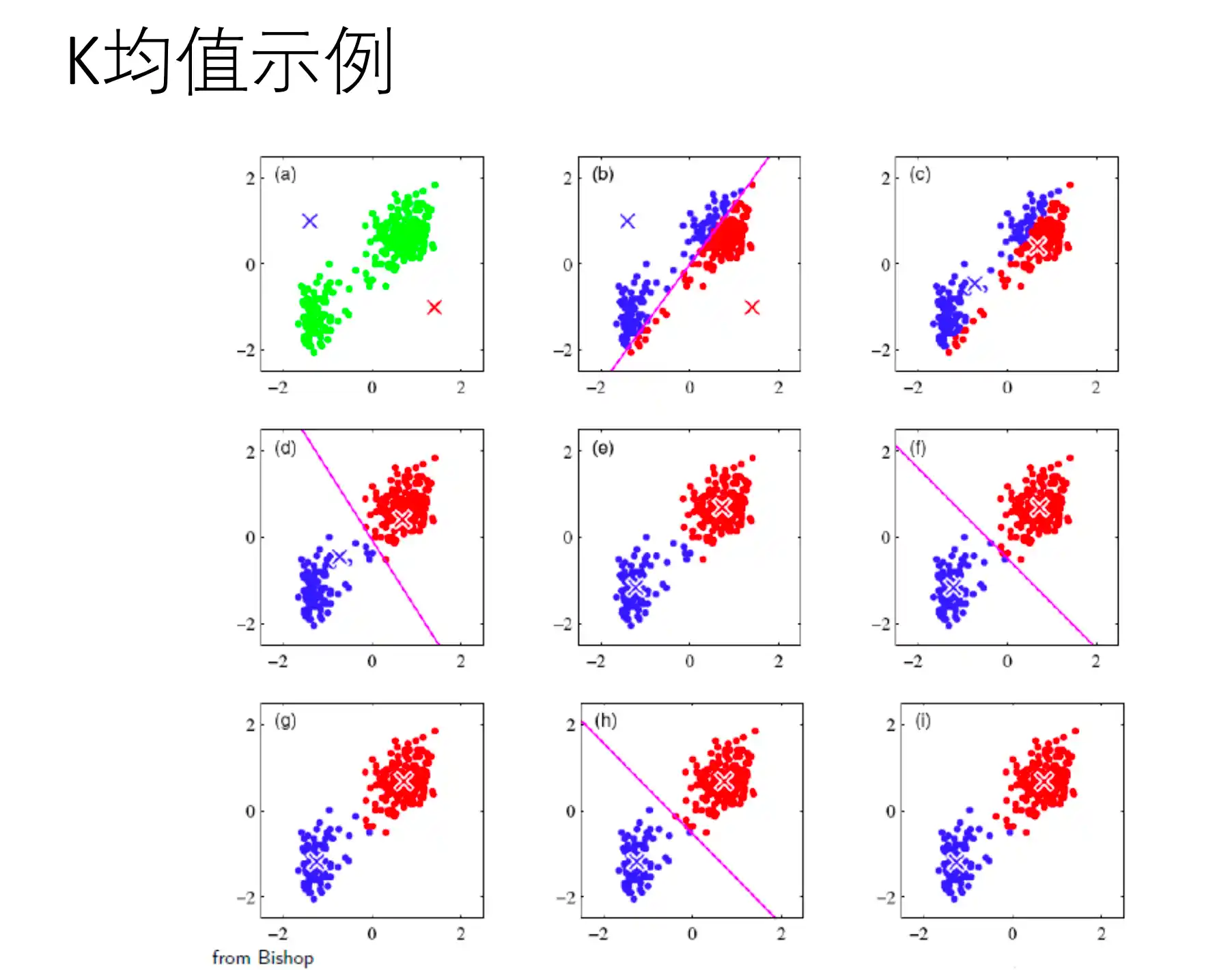
_K均值划分策略



K均值算法实现


K均值算法特点




第八章 混合模型与期望最大
EM算法流程、收敛性以及应用
DEF:
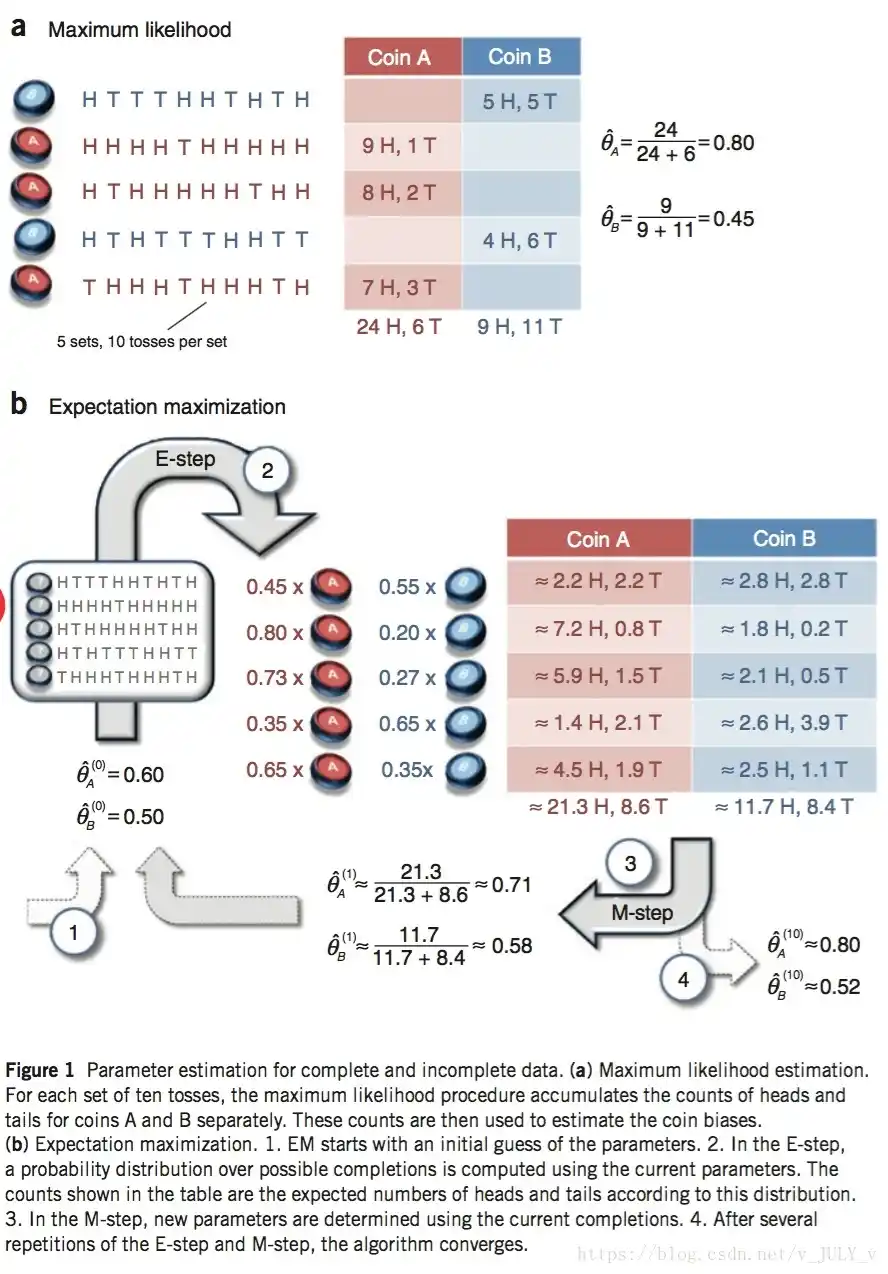
最大期望算法(Expectation-maximization algorithm,又译为期望最大化算法),是在概率模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐性变量。最大期望算法经过两个步骤交替进行计算,==第一步==是计算期望(E),利用对隐藏变量的现有估计值,计算其最大似然估计值;==第二步==是最大化(M),最大化在E步上求得的最大似然值来计算参数的值。M步上找到的参数估计值被用于下一个E步计算中,这个过程不断交替进行。
举个例子:
如果要统计一个学校男女生身高体重的分布,男生的分布和女生肯定是两个不同的分布,但是如果数据中只有身高体重Y 并未标注 男生女生Z 那么如果要找到男生女生的分布就 比较困难, EM算法就是为了解决这种问题
理解:
通过 估计的 隐变量 的先验 计算 所有观测数据Y 的 似然概率 然后用 最大似然 得到 每条Y 最有可能对应的 Z 的值,然后 根据估计过后数据 更新 Z 的估计先验 重复迭代这个过程 (实际上这个Z不是一个常量 而是一个随机变量)
EM算法流程


_EM特点

EM算法的收敛性





EM算法的应用
- EM算法在⾼斯混合模型学习
- EM在伯努利混合模型上的应用
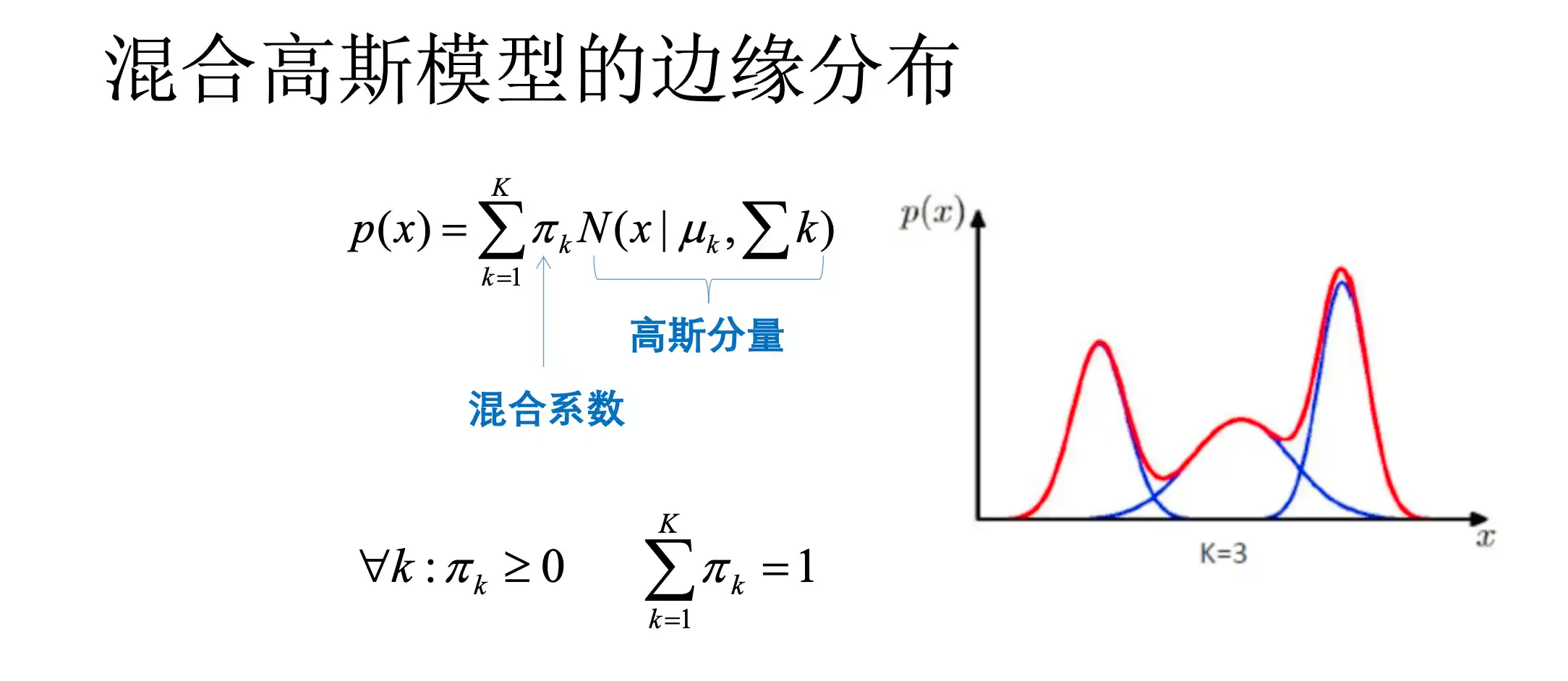
混合高斯模型GMM的原理和特点







PPT:
具体内容找PPT
第九章 神经网络与深度学习
介绍
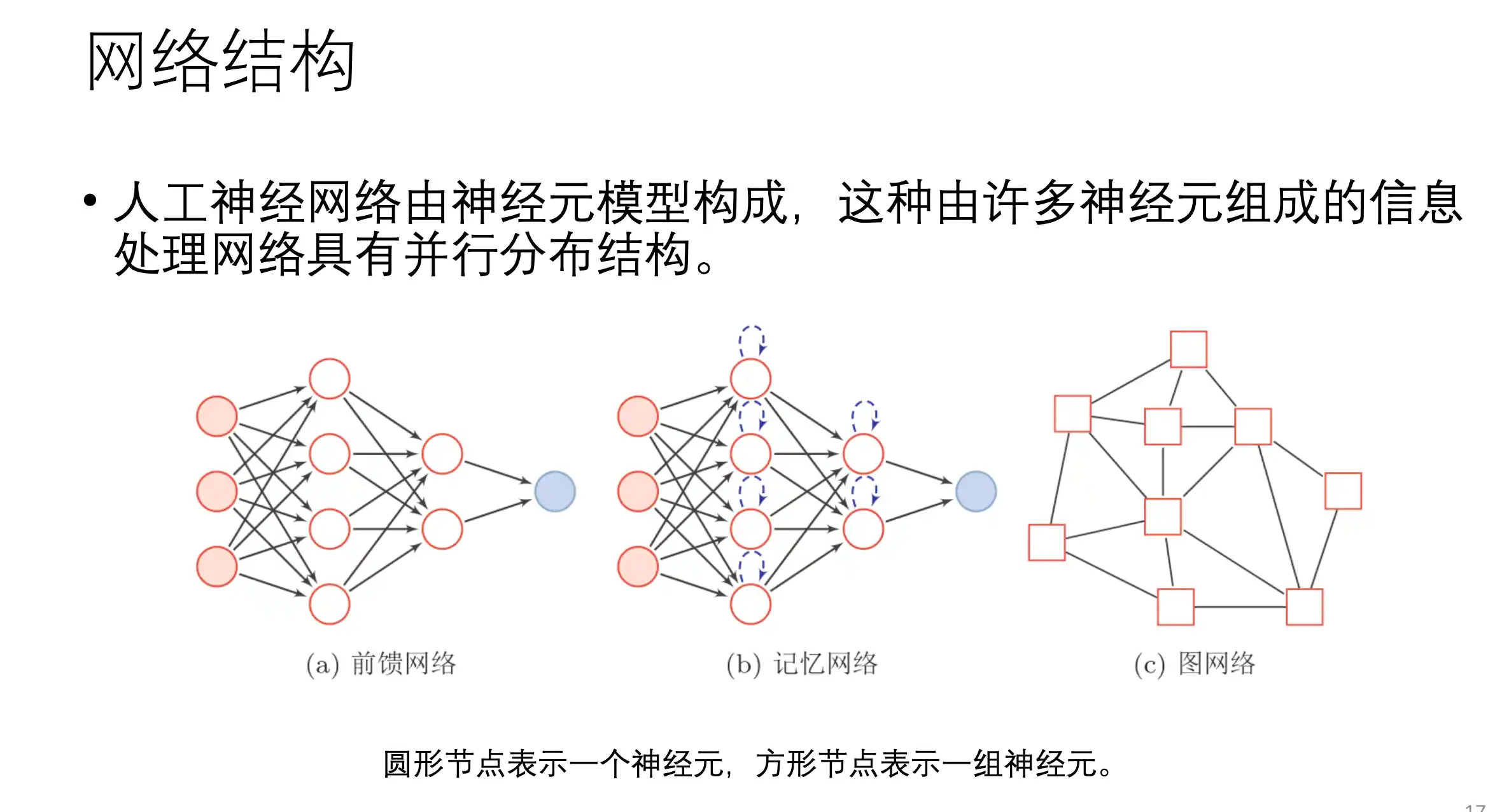
神经网络的要素:
网络结构:
前馈神经网络、梯度下降算法、BP反向传播算法流程
前馈神经网络(全连接神经网络,MLP)
整个网络中没有反馈 全部是正向连接
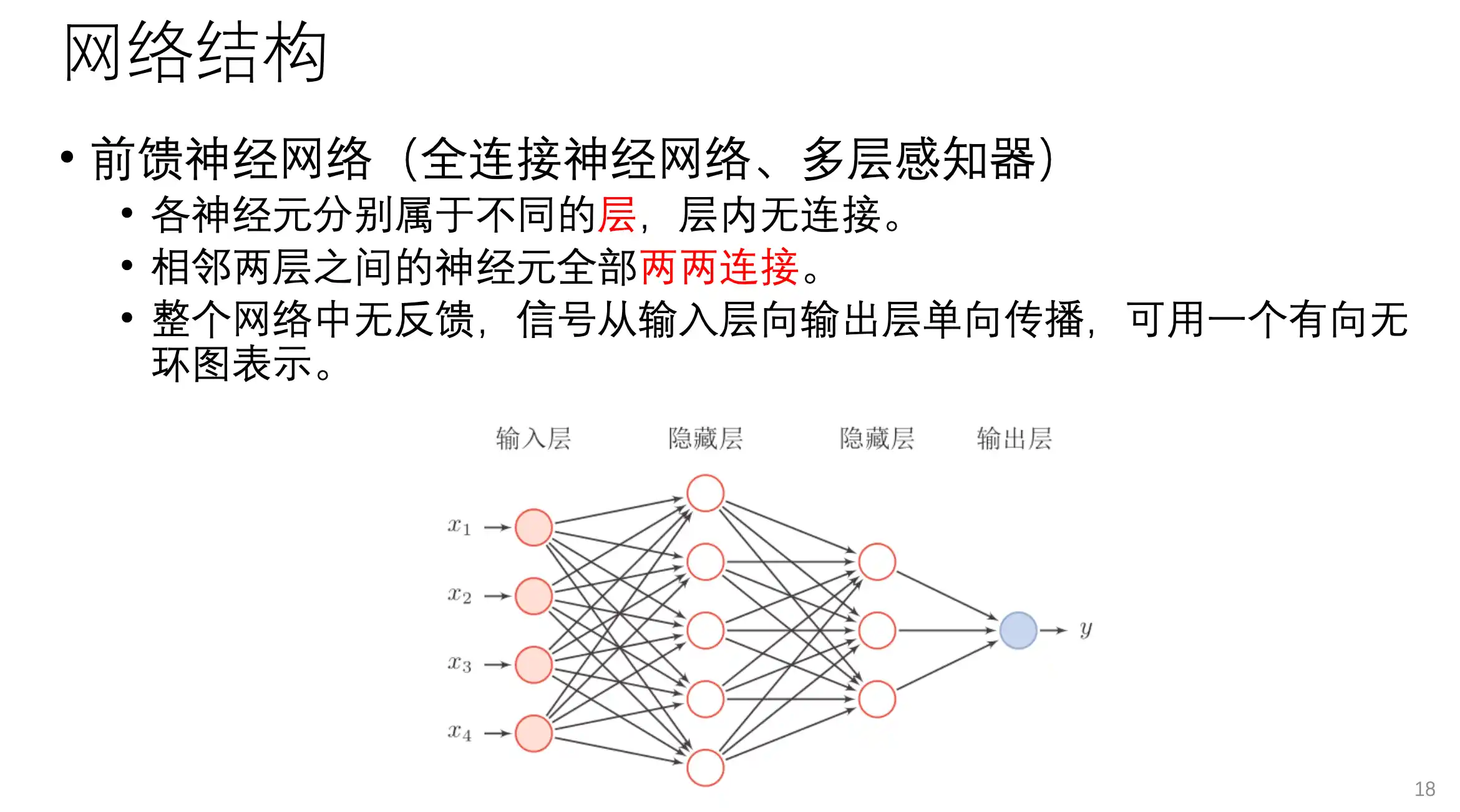

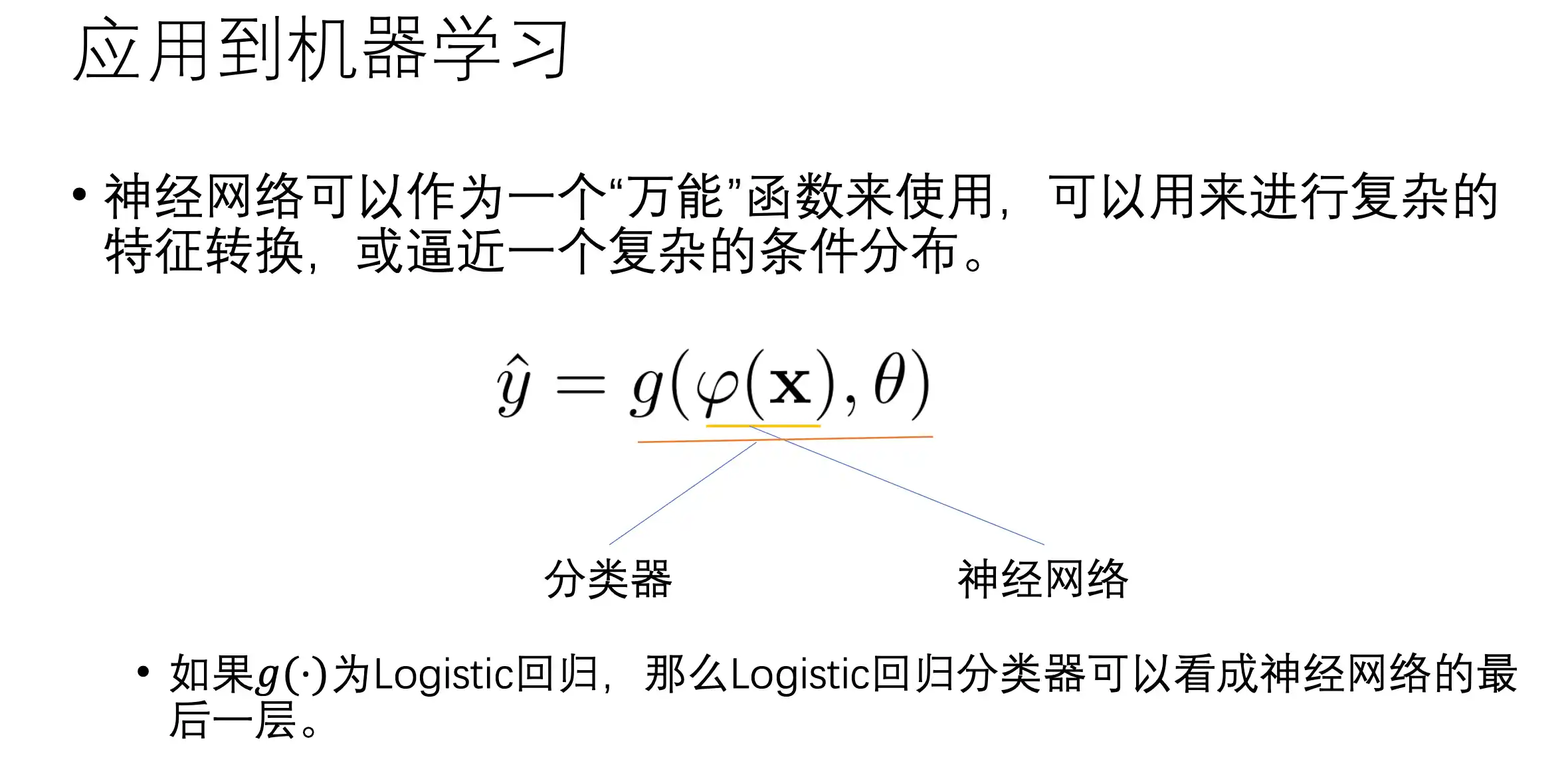
全连接神经网络的缺点
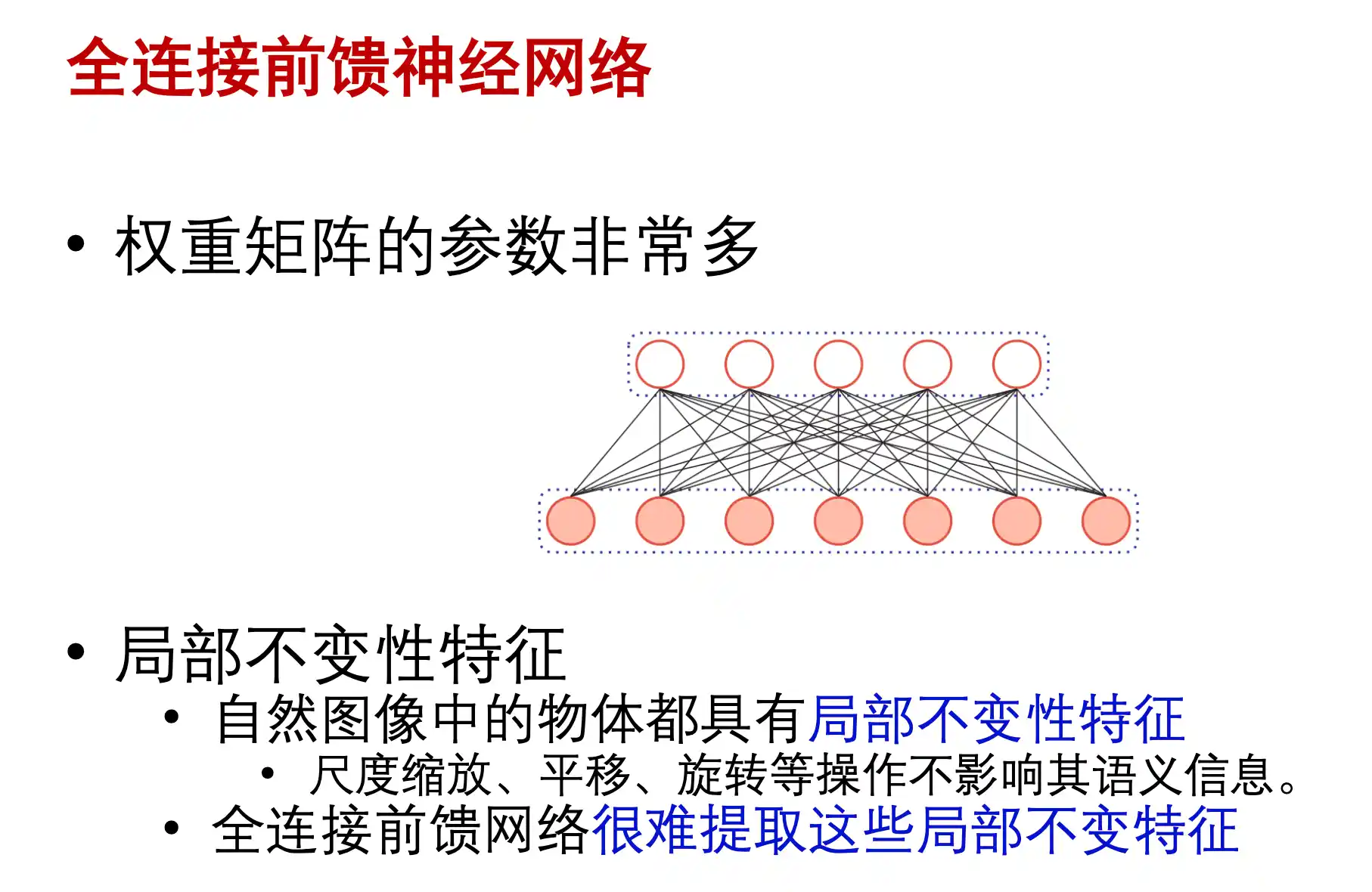

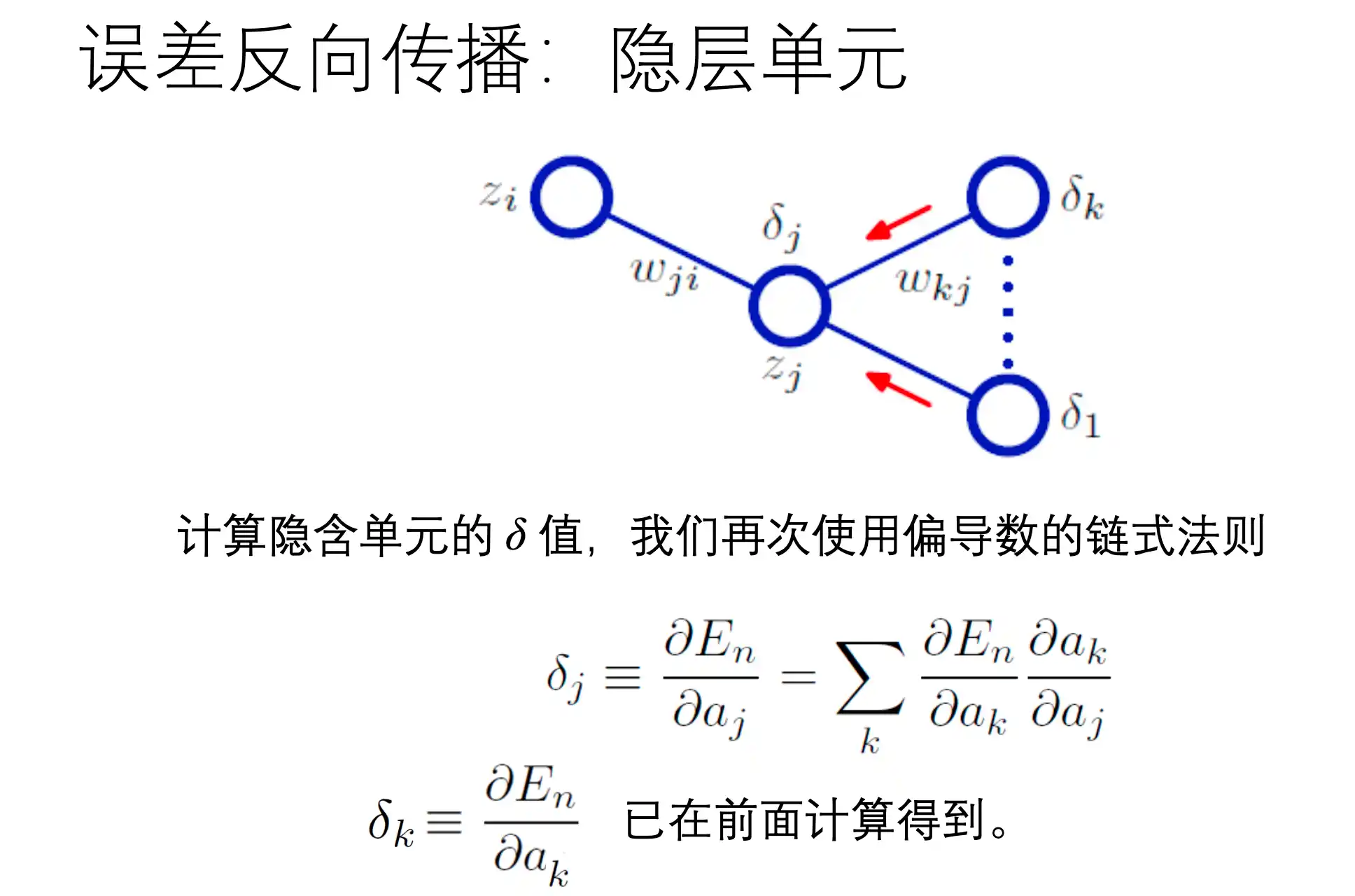
BP反向传播算法
对每个权重求梯度
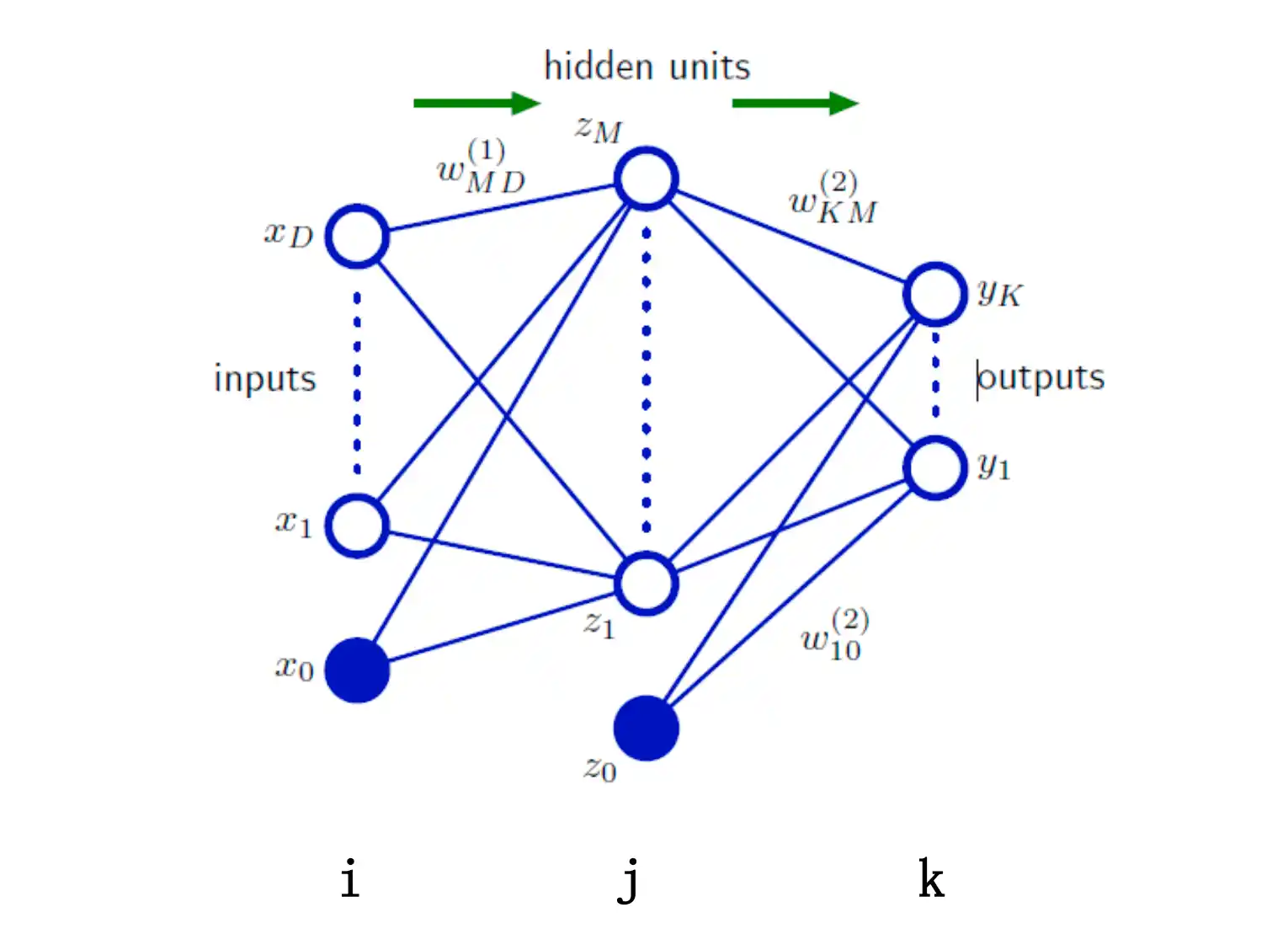
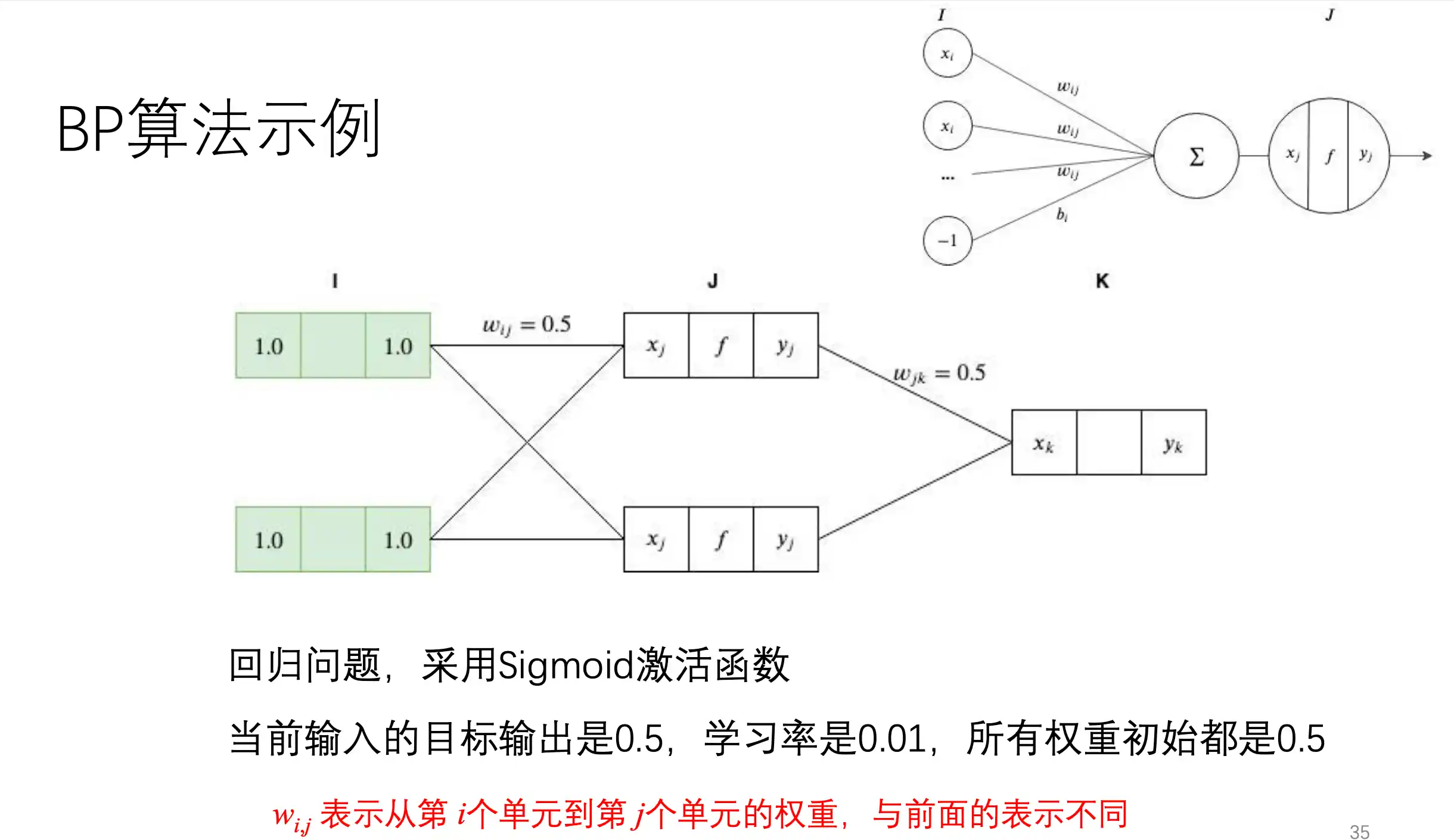
构造一个两层的Net
BP算法原理
前向过程
在上面正向传播过程中,loss对wij的梯度为:


也就是 E 对一个权重 第J层第I个w 的梯度:
???为什么不是这种形式??如果relu的斜率是1 上面下面基本相等了
| 符号 | 意义 | 举例 |
|---|---|---|
| a | 还没激活的加权和 | |
| z | 激活函数后的输出 |



BP算法示例
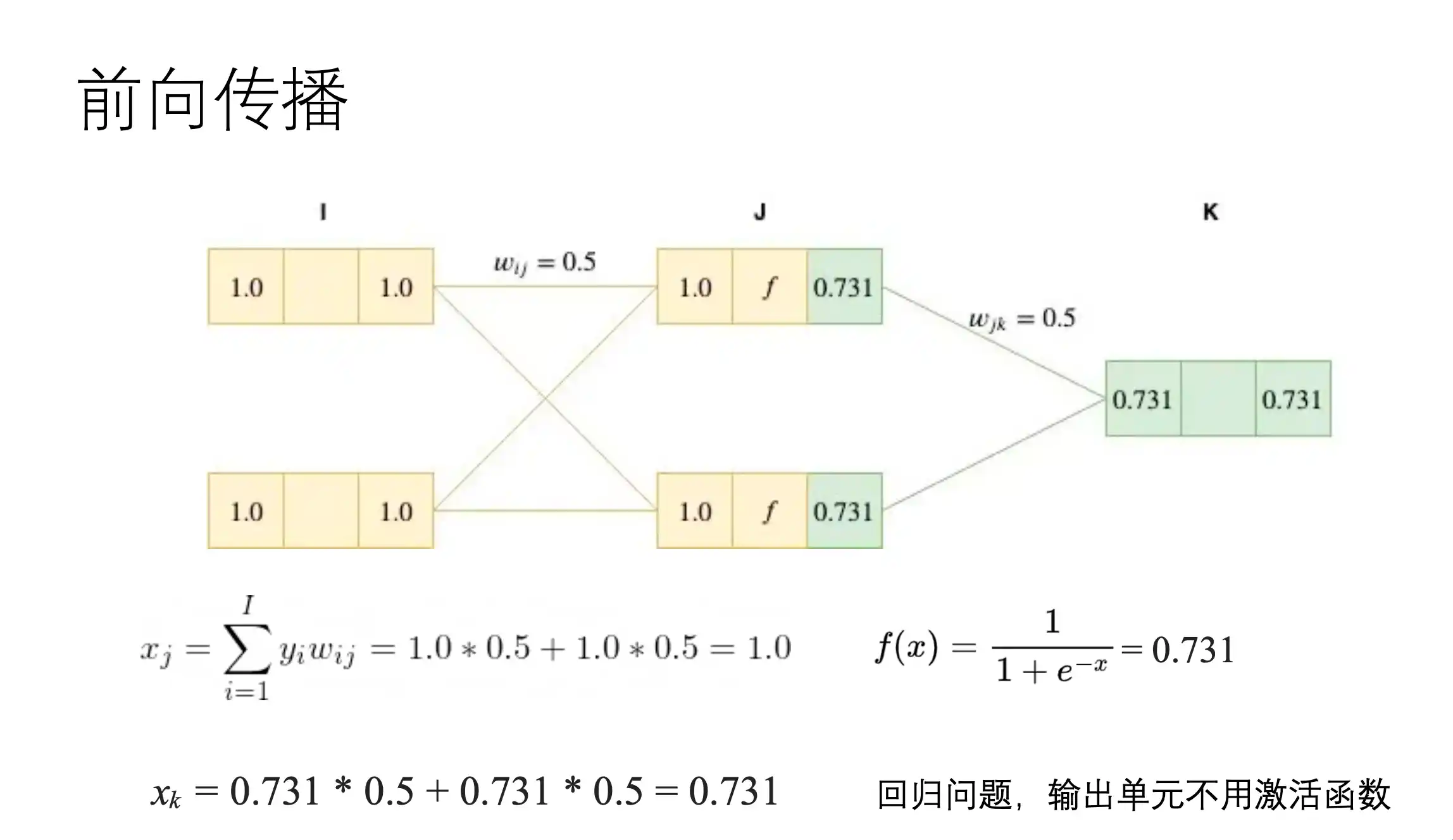
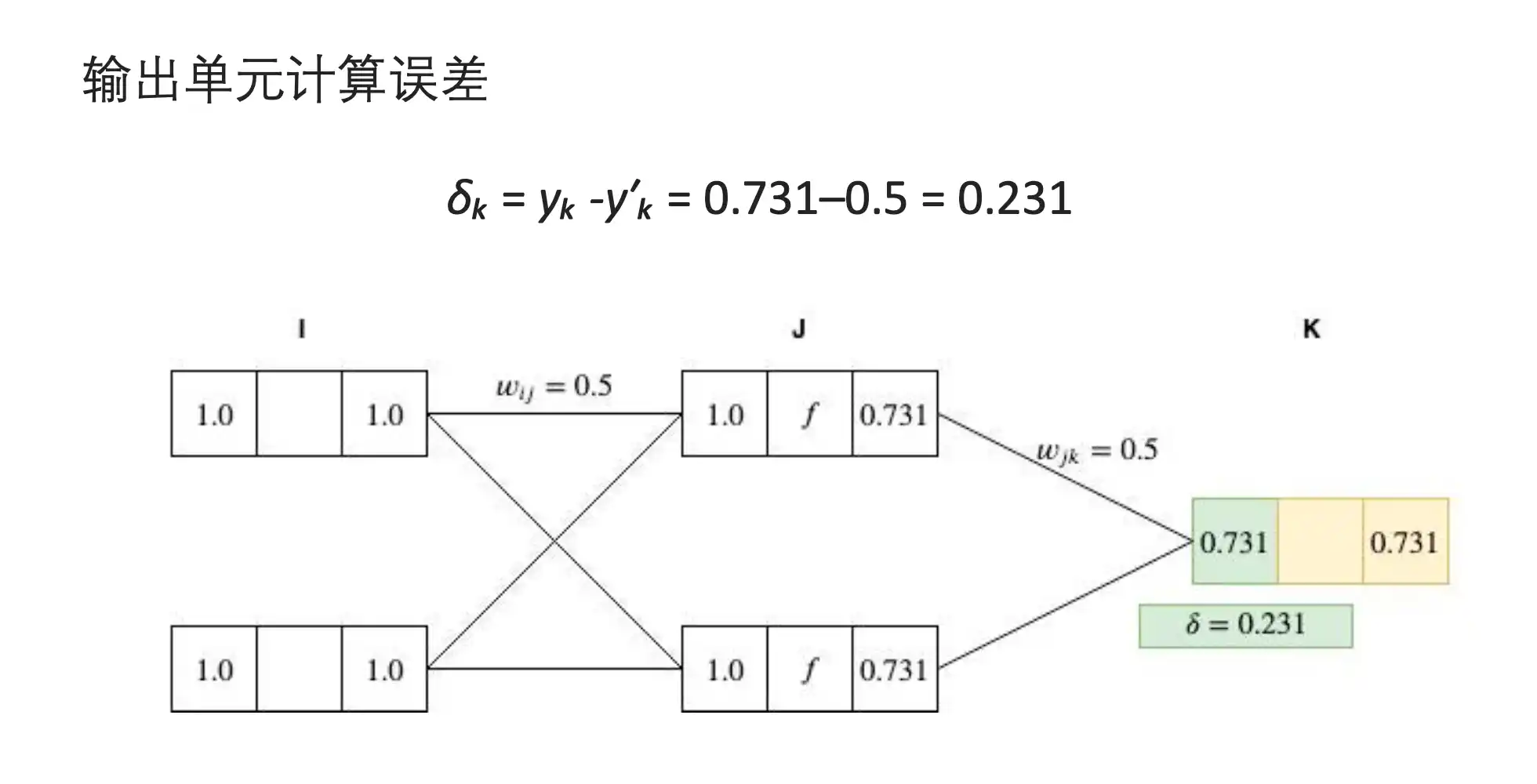
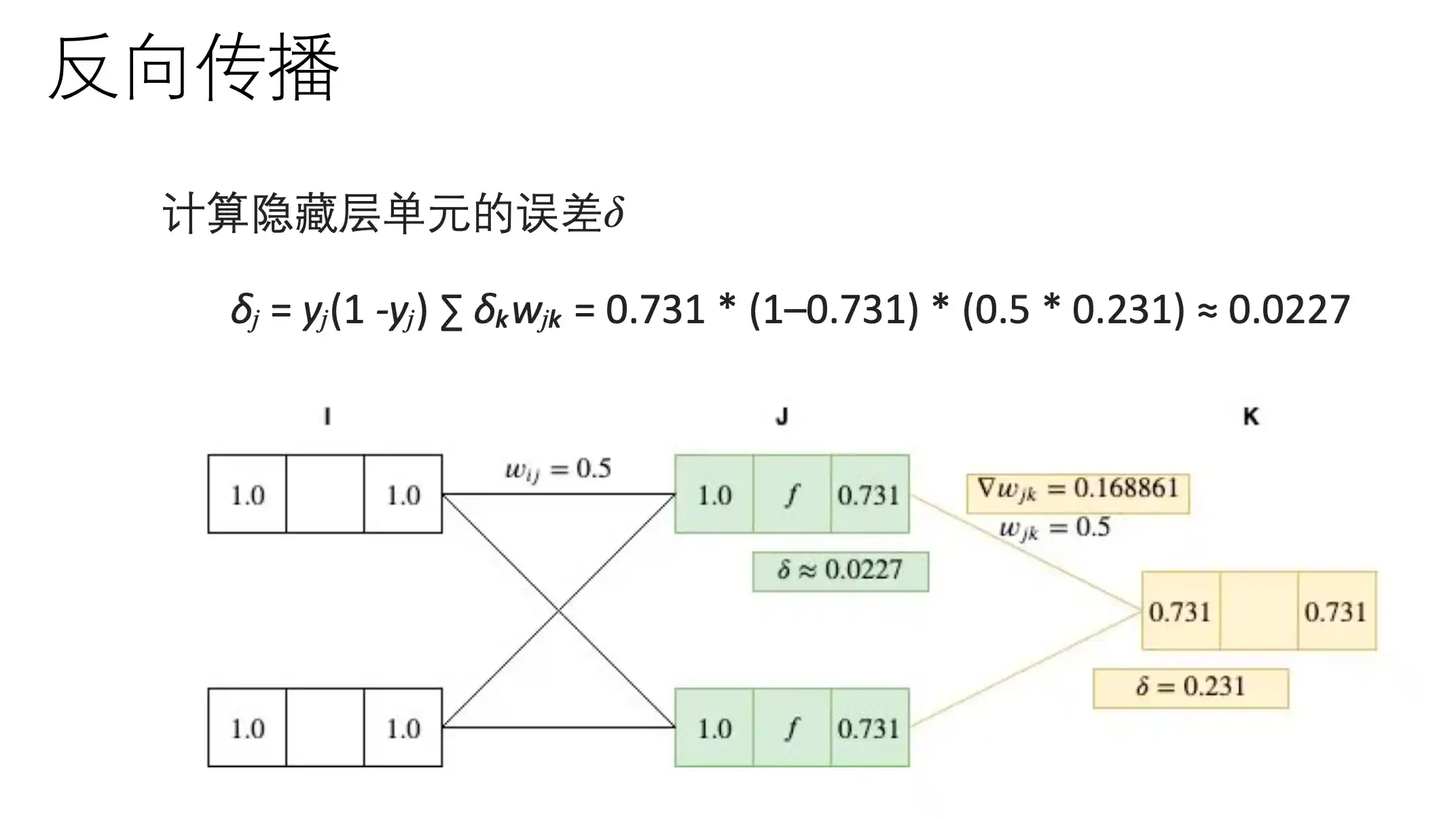
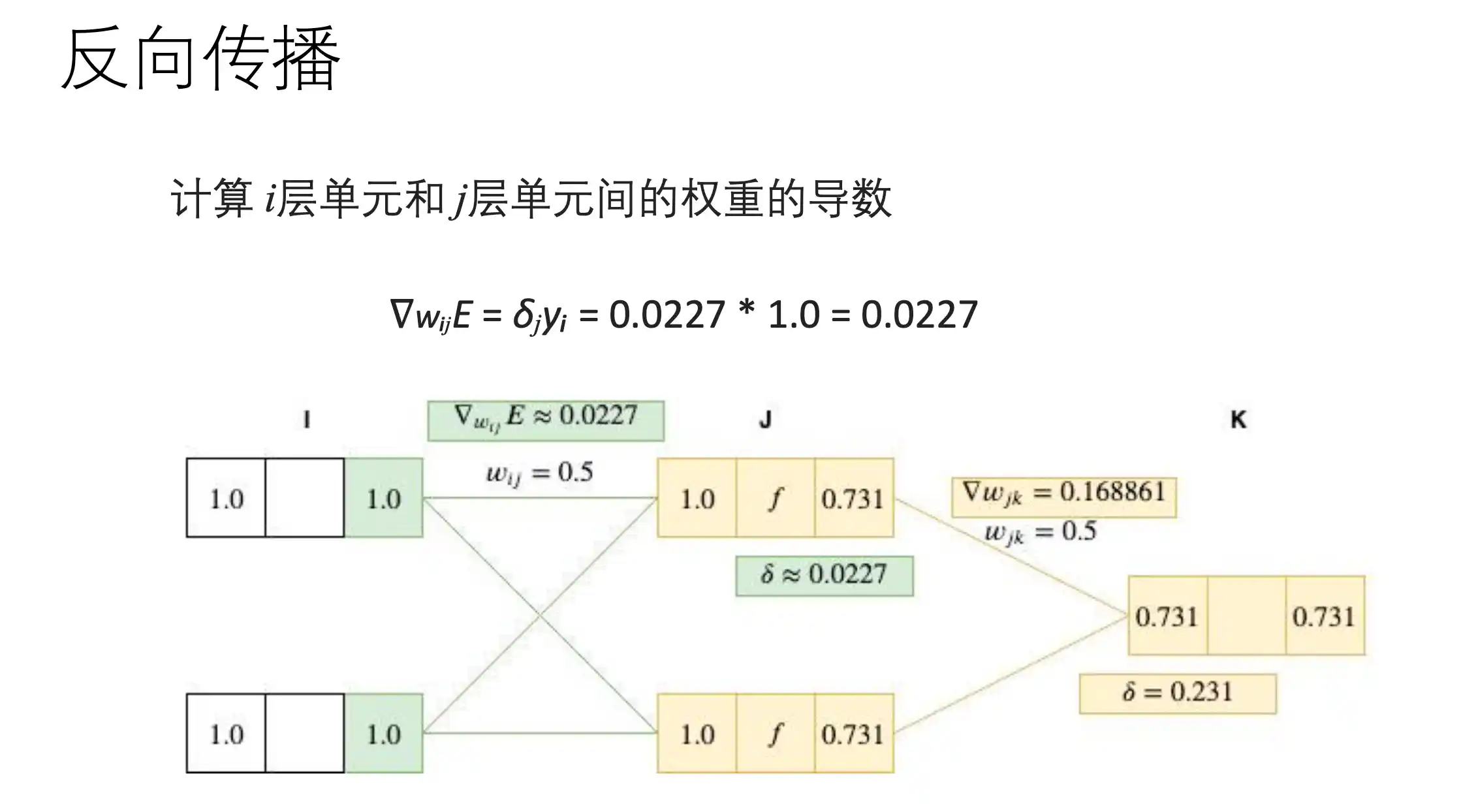

梯度下降算法
李航 附录A 常见的梯度下降算法在 第一章 三要素中
CNN 基本结构,卷积、池化的计算、常用的激活函数
CNN基本结构
上面提到了全链接前馈神经网络的缺点:参数多、局部不变性特征难以提取、展开丢失空间信息、参数多容易过拟合
所以提出了卷积神经网络 CNN 也是一种 前馈神经网络 受生物学上的 感受野机制启发。在结构上有三个特点: 局部感知、权重共享、空间或者时间上的下采样
在视觉神经系统中 一个神经元的感受野 是 指视网膜上的特定区域,只有在这个区域内的刺激才能激活改神经元。
全连接层,导致的参数量过大,浪费资源而且没有这么多的训练数据
局部连接层,在位置相同的地方数据类似(人脸识别)参数量小一些
卷积层,不同位置共享权重,通过可学习的卷积核进行卷积
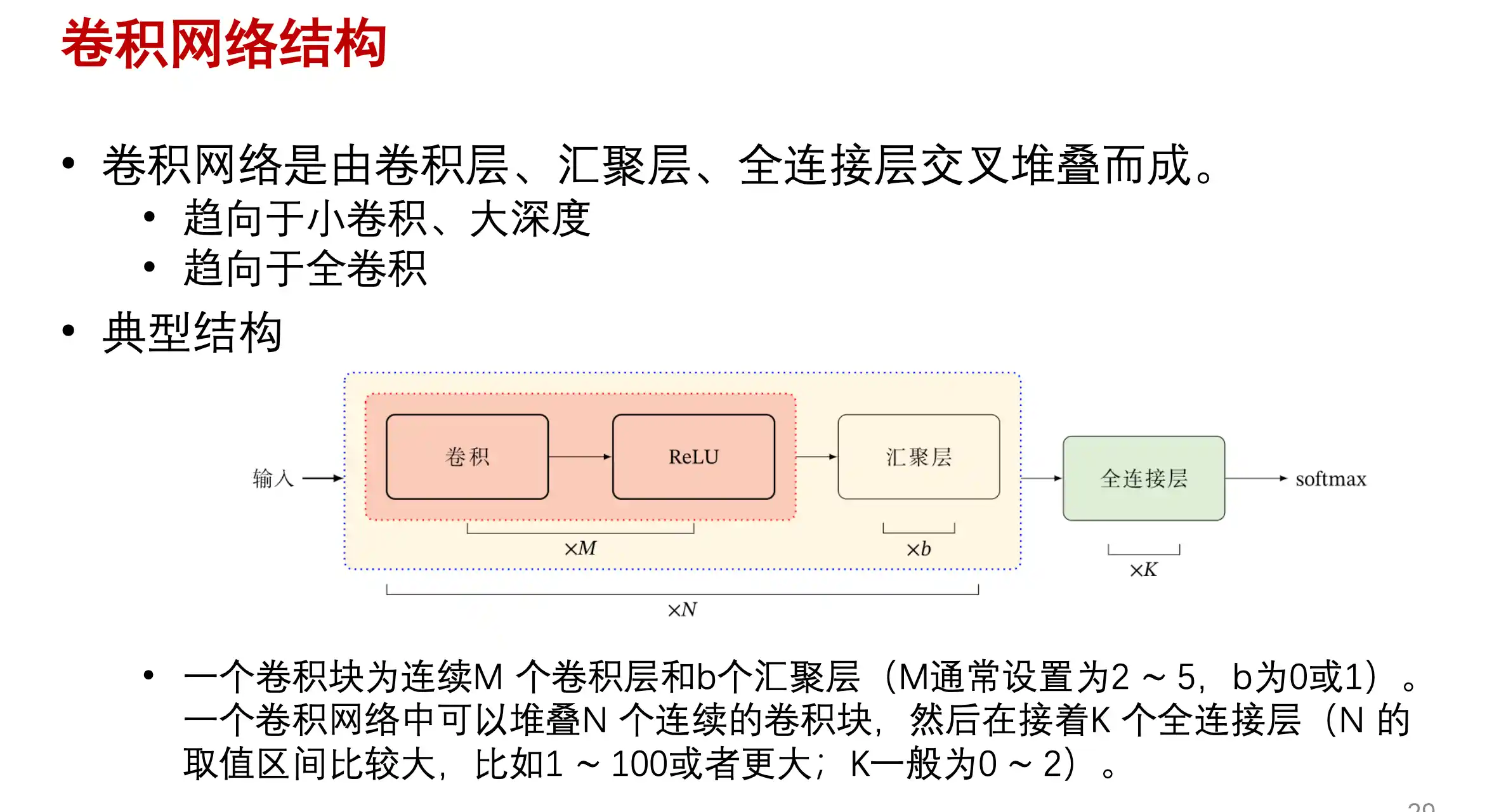
这个里面的汇聚层是 池化

卷积操作 Convolution
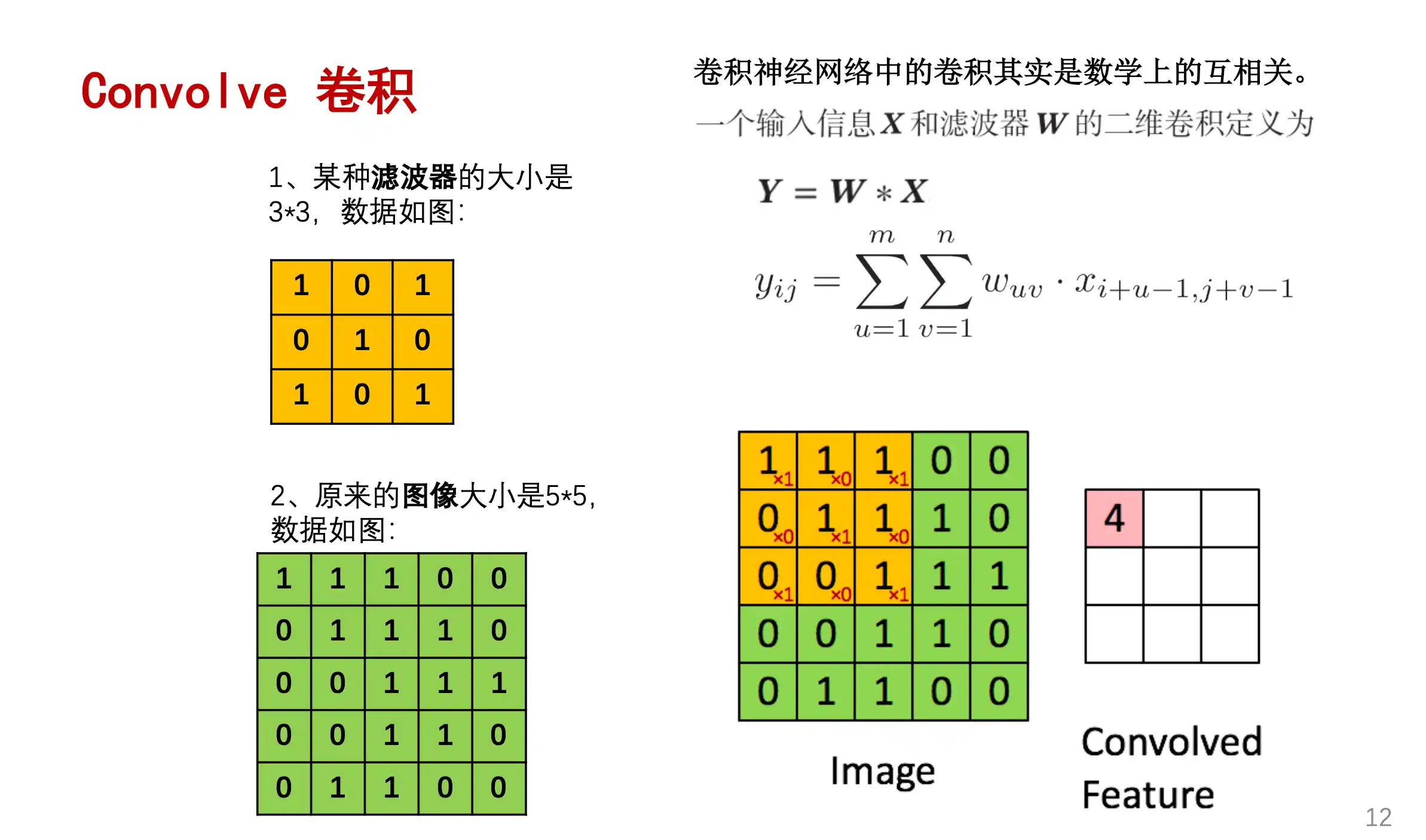

padding就是在外面对图像进行补0操作 stride就是kernel移动的步长是多少。
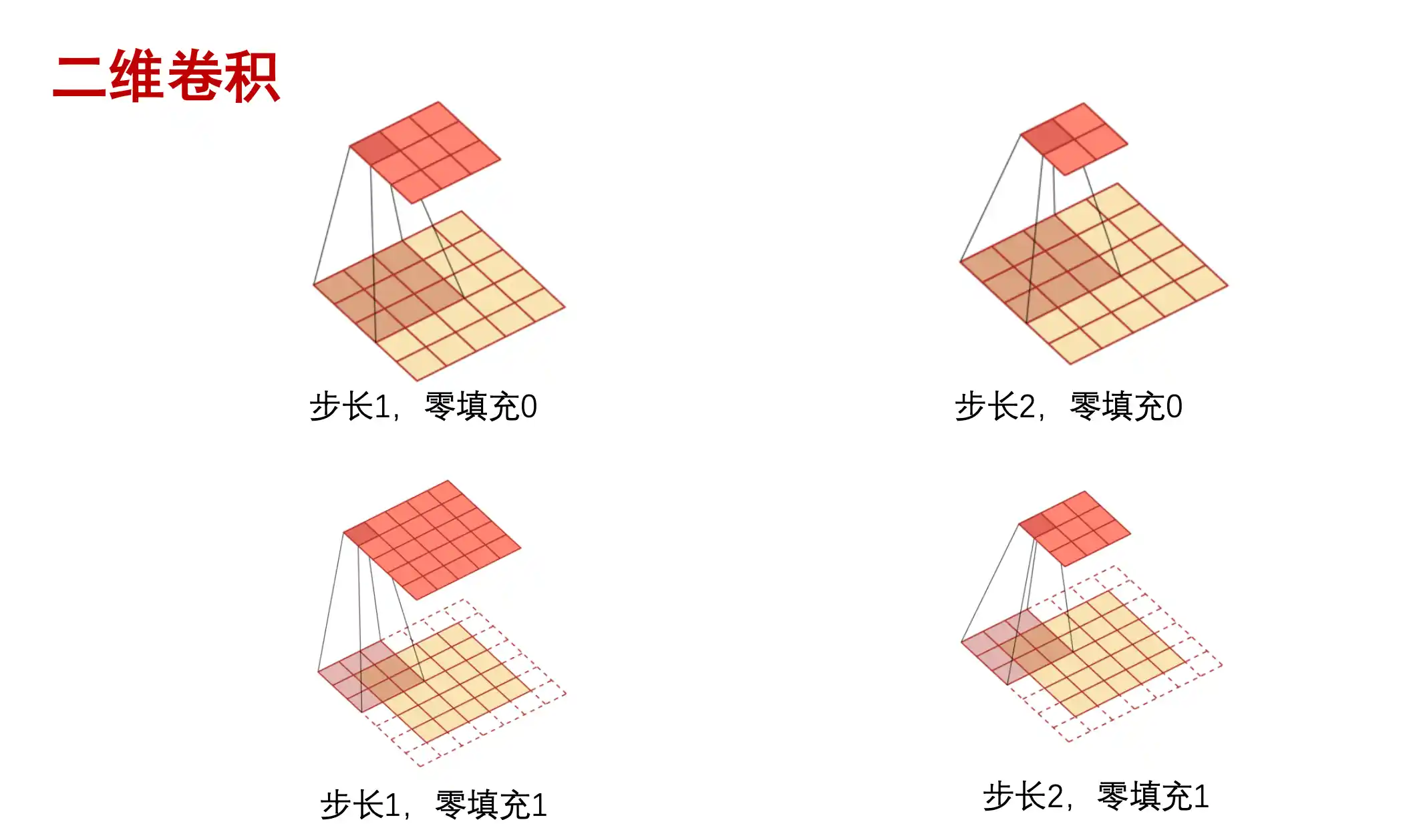
一个卷积核卷出来一层 有多少个卷积核 卷完后通道就是多少 每个卷积核的通道数应该与输入特征图的通道数对齐
卷积后feature map的size
对于给定的输入尺寸
1. 没有填充的情况 (padding = false):
2. 有填充的情况 (padding = true):
对于填充,通常我们使用"same"填充来保证输出尺寸与输入尺寸相同。在这种情况下,填充的大小为:
然后输出尺寸为:
这就是计算输出尺寸
池化 Pooling Layer
1 | 如果我们想让“眼睛检测器”这个滤波器(例如卷积神经网络中的卷积核)对于眼睛的**精确位置**不那么敏感,可以通过 **池化pooling** 操作来提高检测的鲁棒性。 |
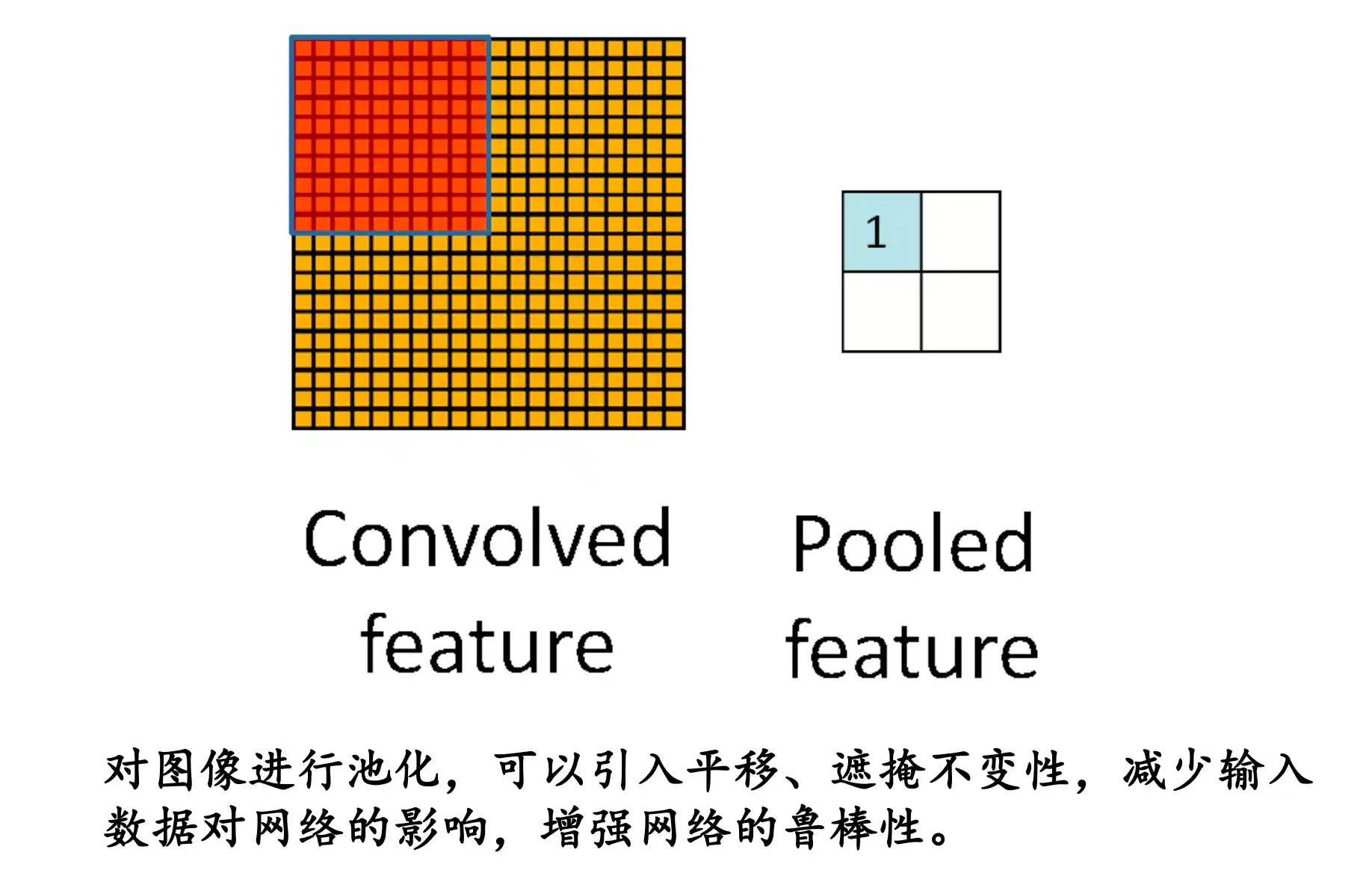
不在关注具体在哪个像素 而是知道在哪个大概区域

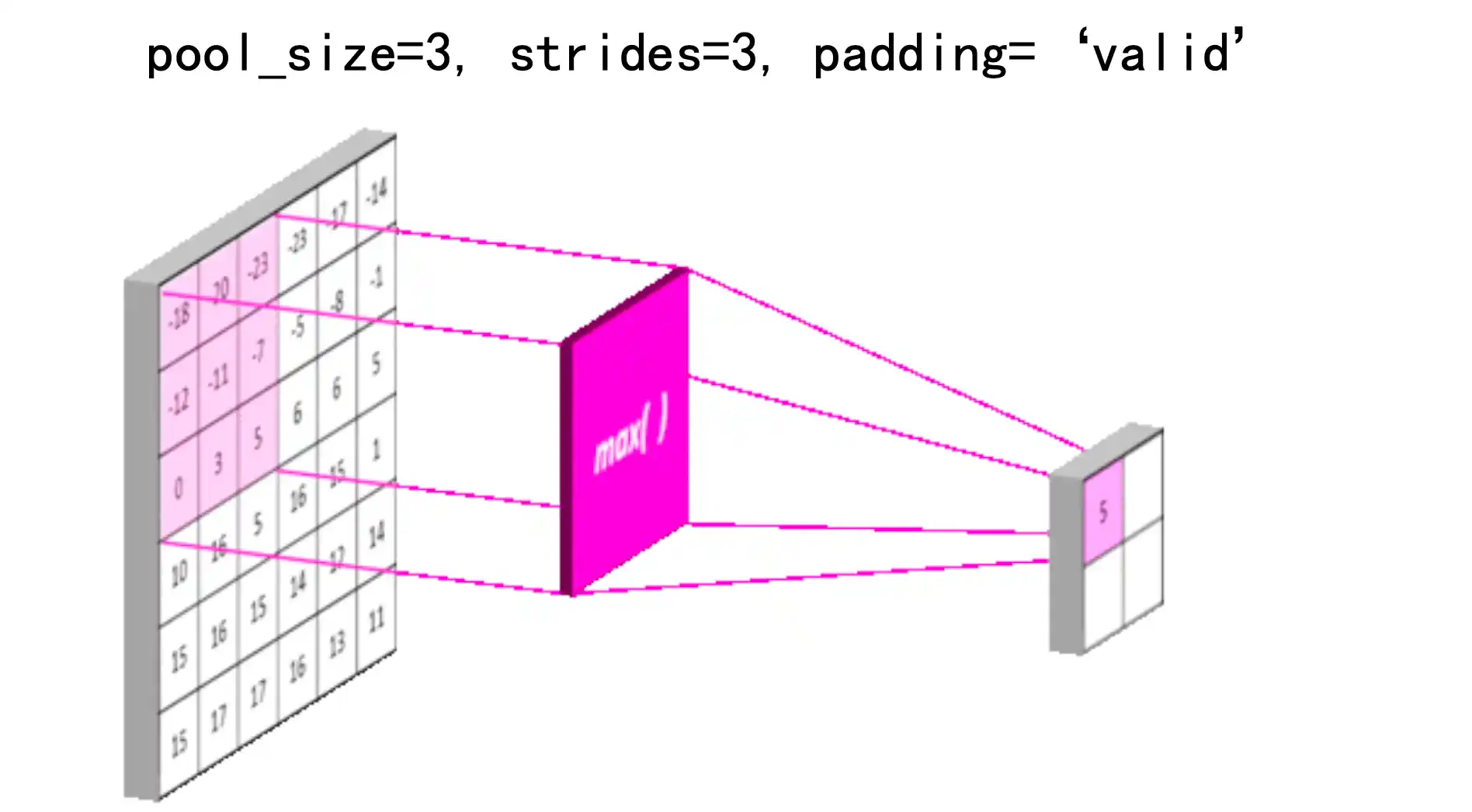
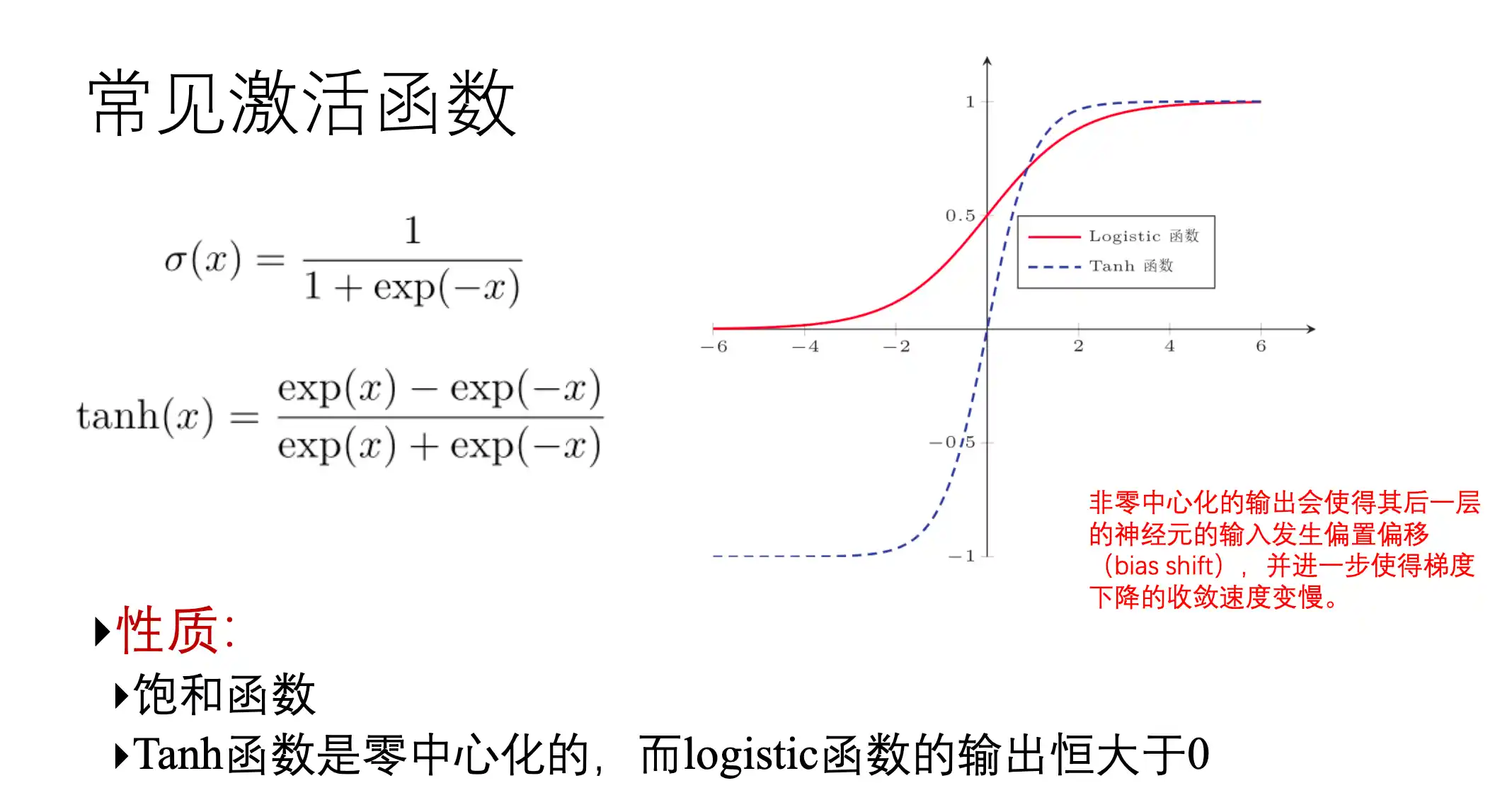
常用的激活函数
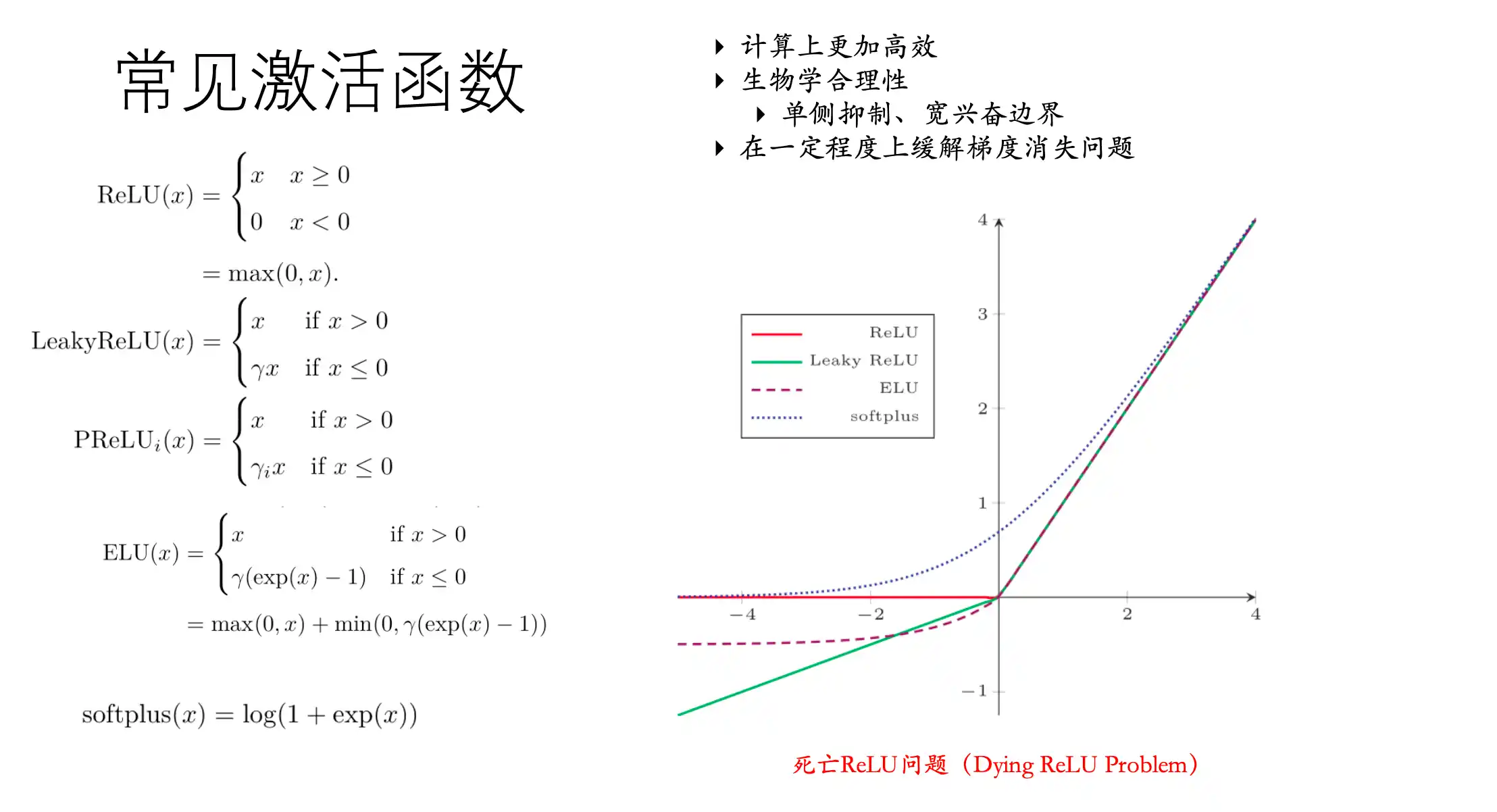

RNN基本结构以及存在的问题、LSTM的基本结构
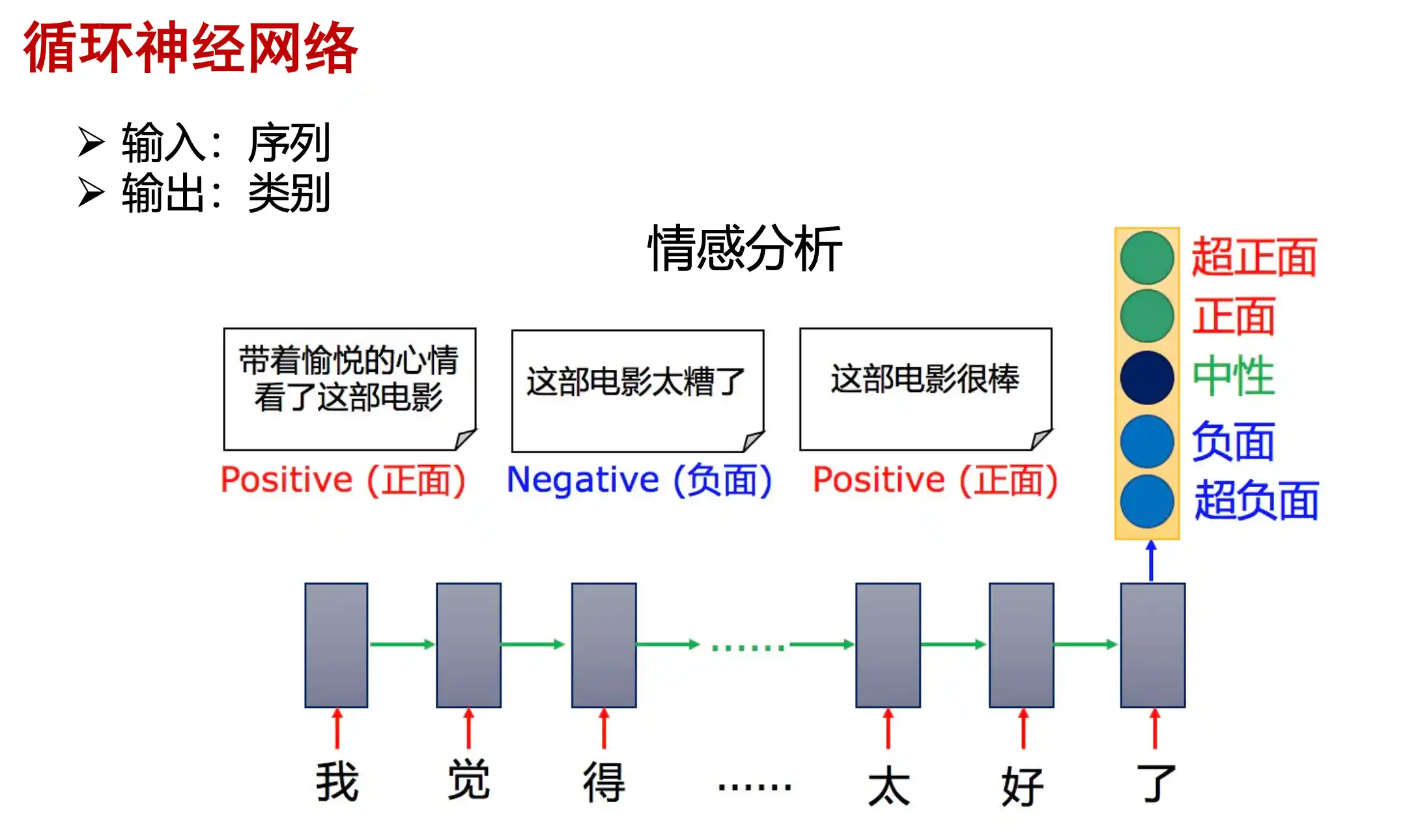
RNN 循环神经网络
由于卷积网络的局限性:1.接受固定长的向量作为输入,产生固定长度的输出;2.计算的数量是固定的
但是有时候需要处理时序和序列的数据,接受和生成变长的输入或输出 因此引出了循环神经网络RNN (Recurrent)
RNN例子
同步就是 输入后输出所有对应位置
异步是输入后逐个输出上一个
循环神经网络的特点

RNN的结构
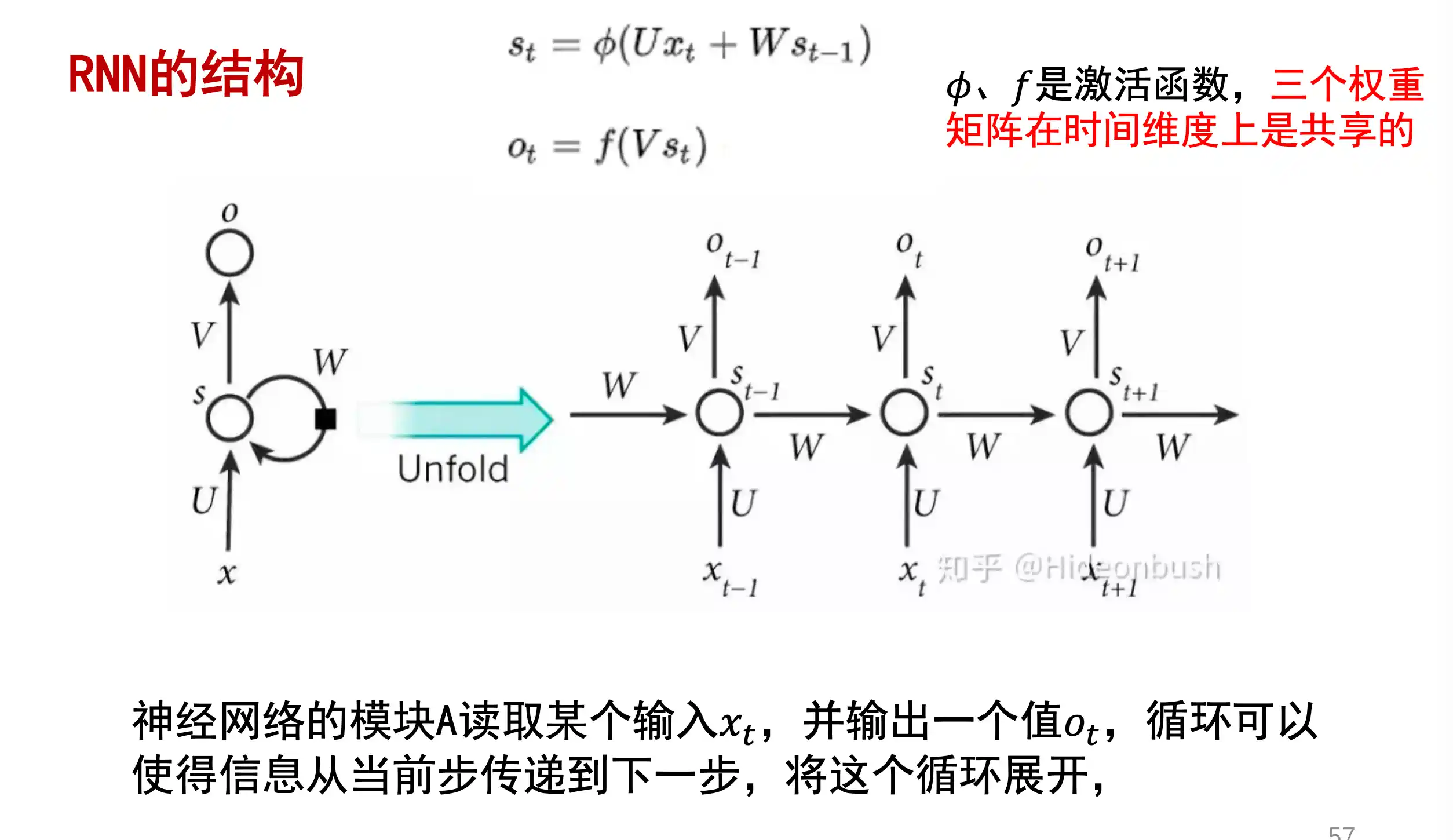
RNN的训练算法
RNN训练时候用BPTT算法


RNN的长期依赖问题
因为上面所示 梯度反向传播中的累乘 很容易出现 梯度消失或者梯度爆炸 ,这是因为RNN在时间维度上非常深。想要改进这个问题,对于梯度爆照:需要用 权重衰减 或者 权重截断 方法 ;对于梯度消失:需要改进模型来解决
直观感受长期依赖
越早的输入影响就越小,越晚的输入影响就越大,而且这个逻辑是固定的,无法改变。
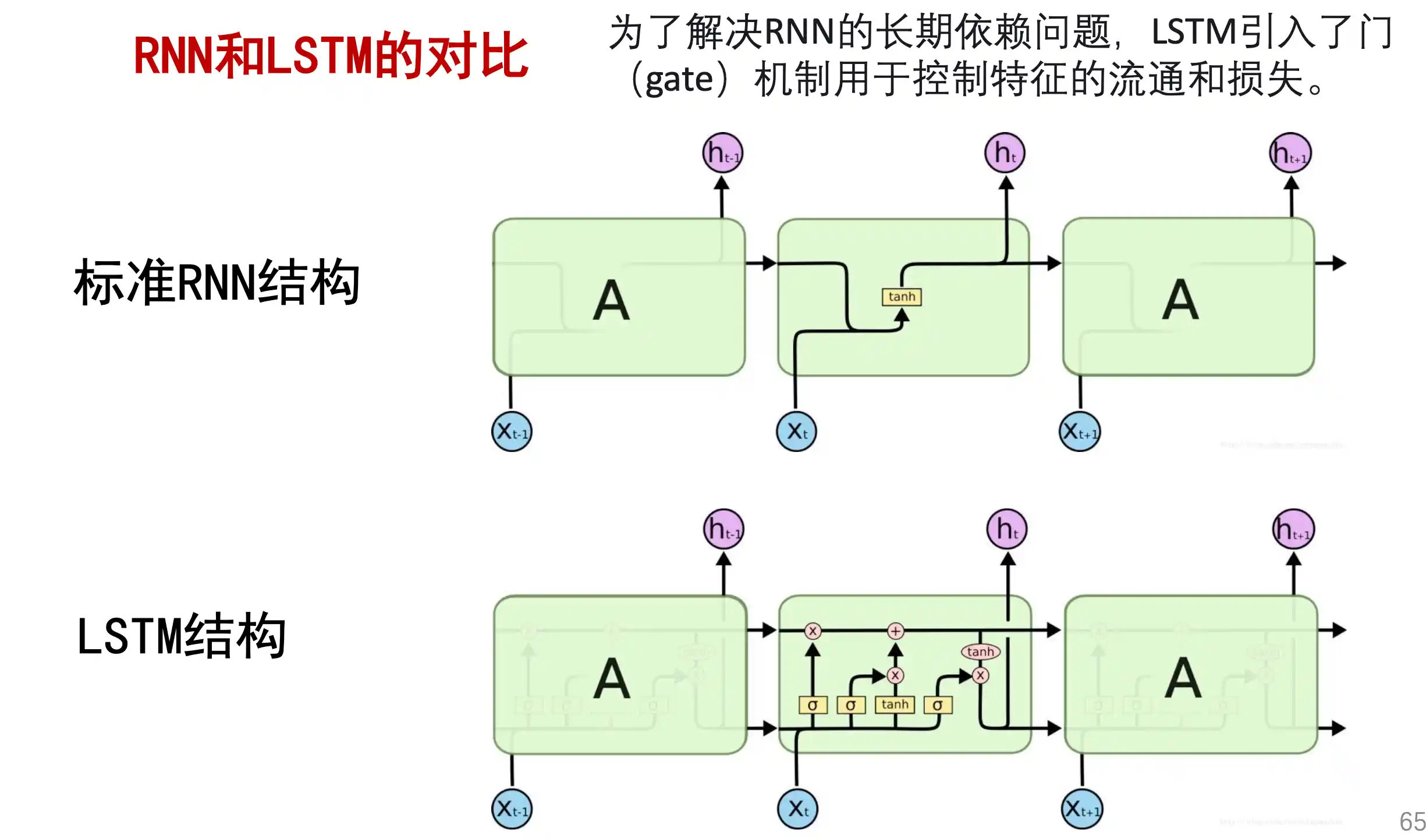
LSTM 长短期记忆网络
为了解决上面 RNN 对早晚输入注意程度不一致,而且逻辑无法改变的问题 ,引入了LSTM。
LSTM 保留了较长序列中的 重要信息,忽略不重要的信息。这样就解决了 RNN 的短期记忆的问题。

LSTM 的基本结构
LSTM的思想:
LSTM vs RNN :
下图中:
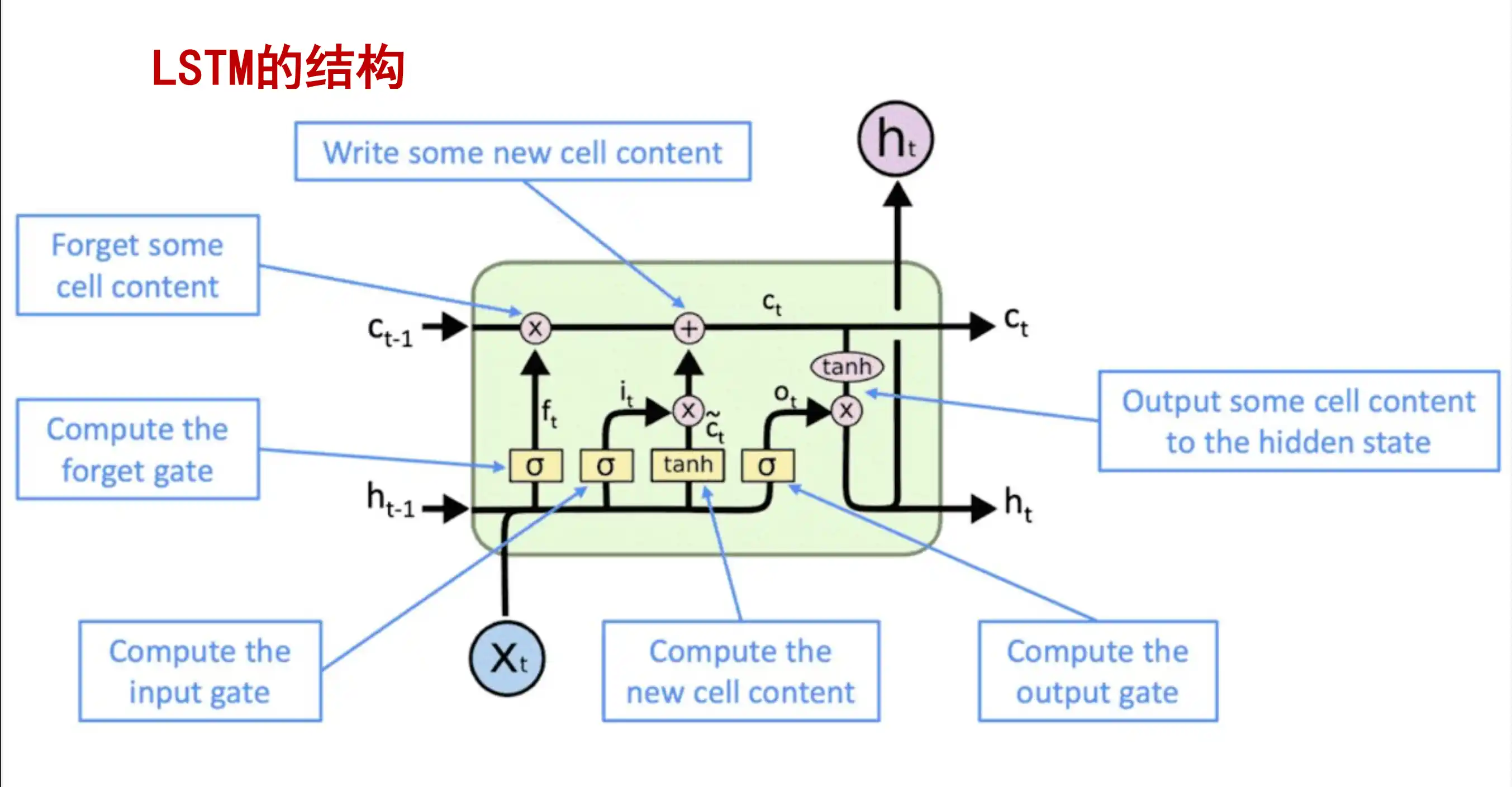
指出了 LSTM(长短期记忆网络)中的以下关键部分:
1. Write some new cell content(写入新的细胞状态内容)
- 对应 输入门(Input Gate) 的计算,决定哪些新信息会被存储到细胞状态中。
2. Forget some cell content(遗忘部分细胞状态内容)
- 对应 遗忘门(Forget Gate) 的计算,决定哪些旧信息会被丢弃。
3. Compute the forget gate(计算遗忘门)
- 明确提到遗忘门的操作,通过 sigmoid 函数决定保留或遗忘多少历史信息。
4. Compute the input gate(计算输入门)
- 明确提到输入门的操作,通过 sigmoid 函数决定更新哪些新信息。
5. Compute the new cell content(计算新的细胞状态内容)
- 结合输入门和候选细胞状态(通常由 tanh 函数生成),更新细胞状态。
6. Compute the output gate(计算输出门)
- 对应 输出门(Output Gate) 的计算,通过 sigmoid 函数决定输出哪些信息,再结合 tanh 处理的细胞状态生成最终输出。
7. 候选细胞状态(Candidate Cell State):通常由当前输入和前一隐藏状态通过 tanh 函数生成,用于后续细胞状态更新。
8. 隐藏状态(Hidden State):作为 LSTM 的输出,传递到下一时间步或网络层。





Transformer基本结构以及特点
Attention
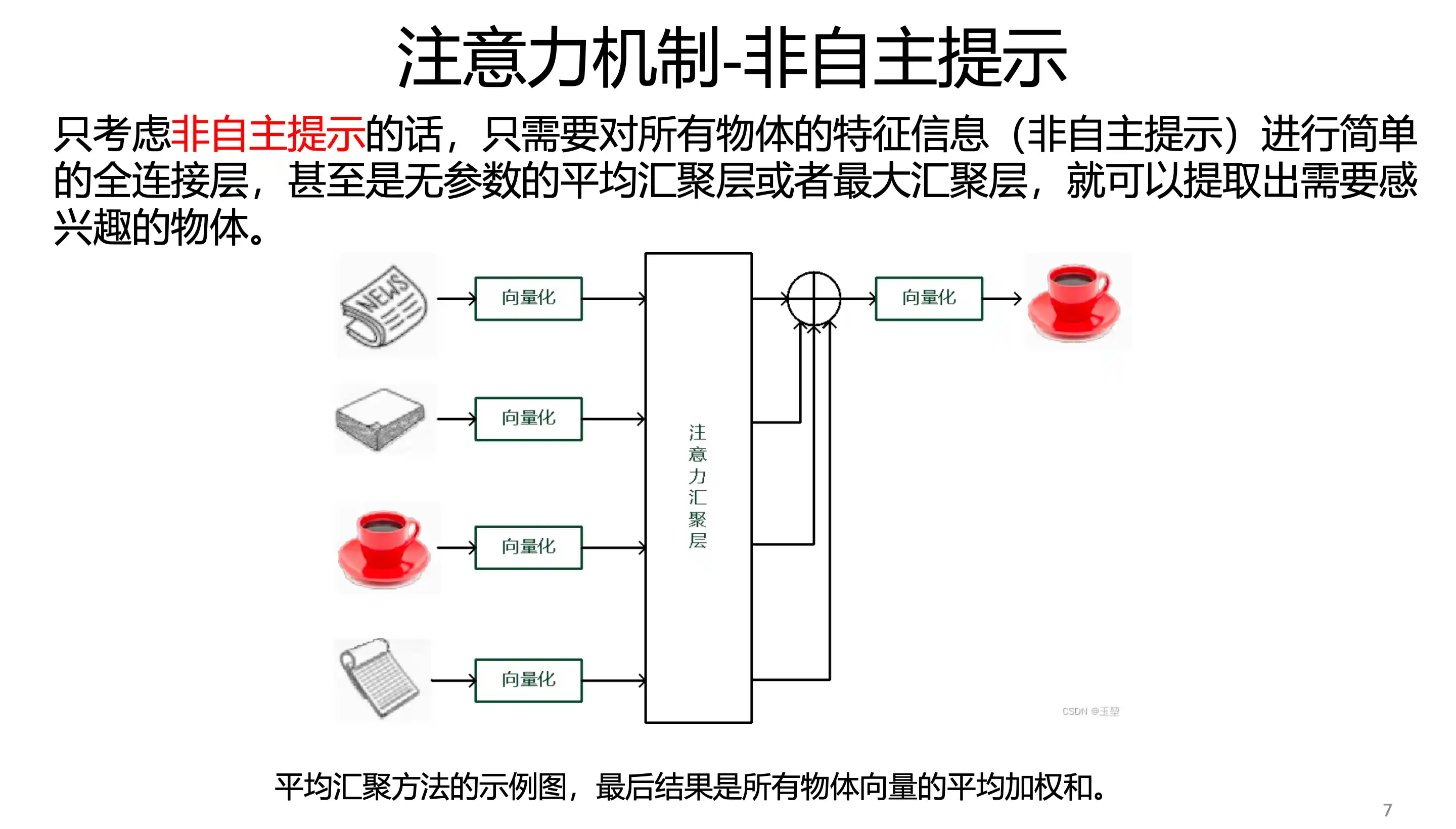
非自主提示 无参数汇聚(最大 平均池化)
自主提示 注意力机制
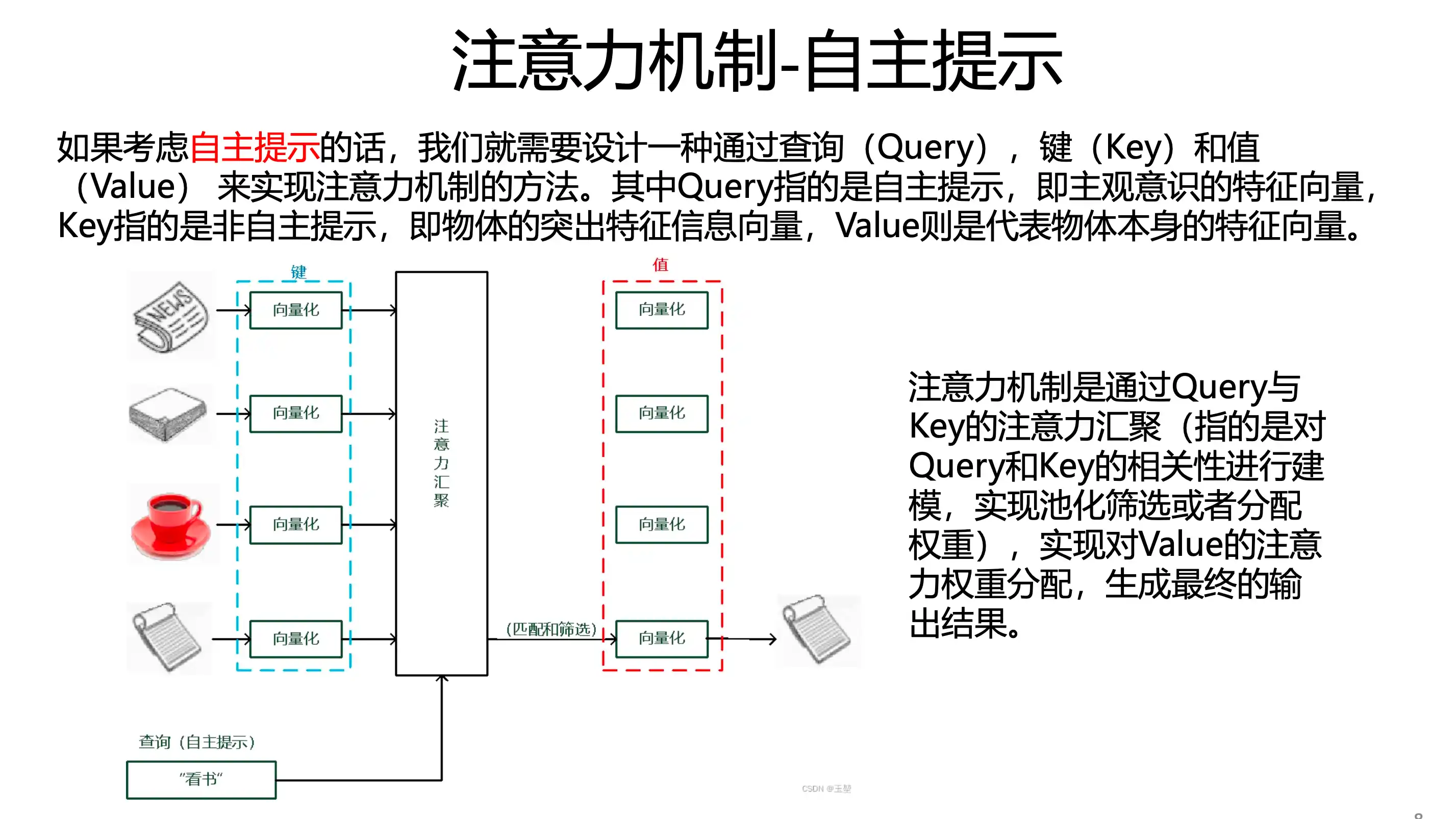
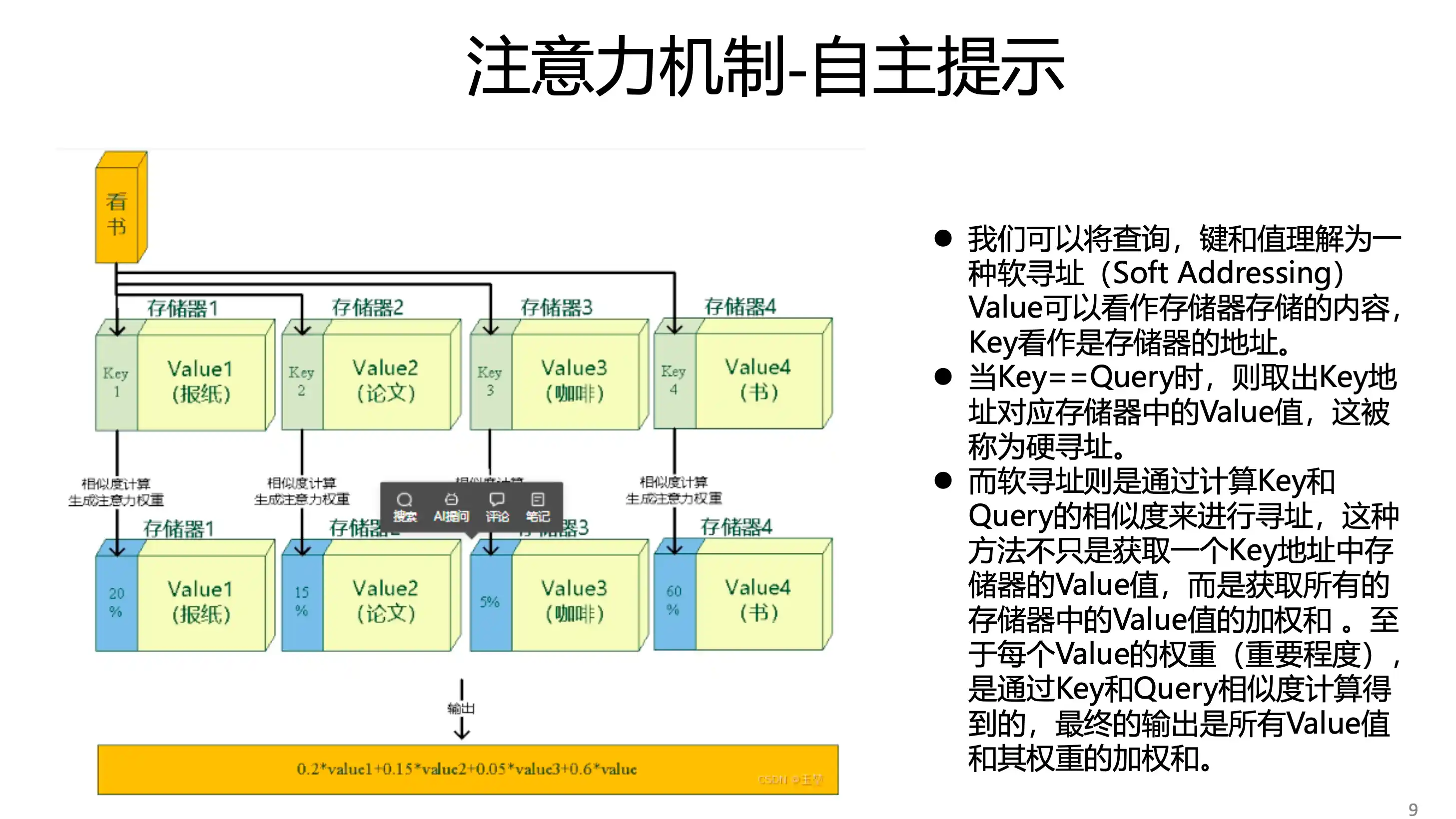
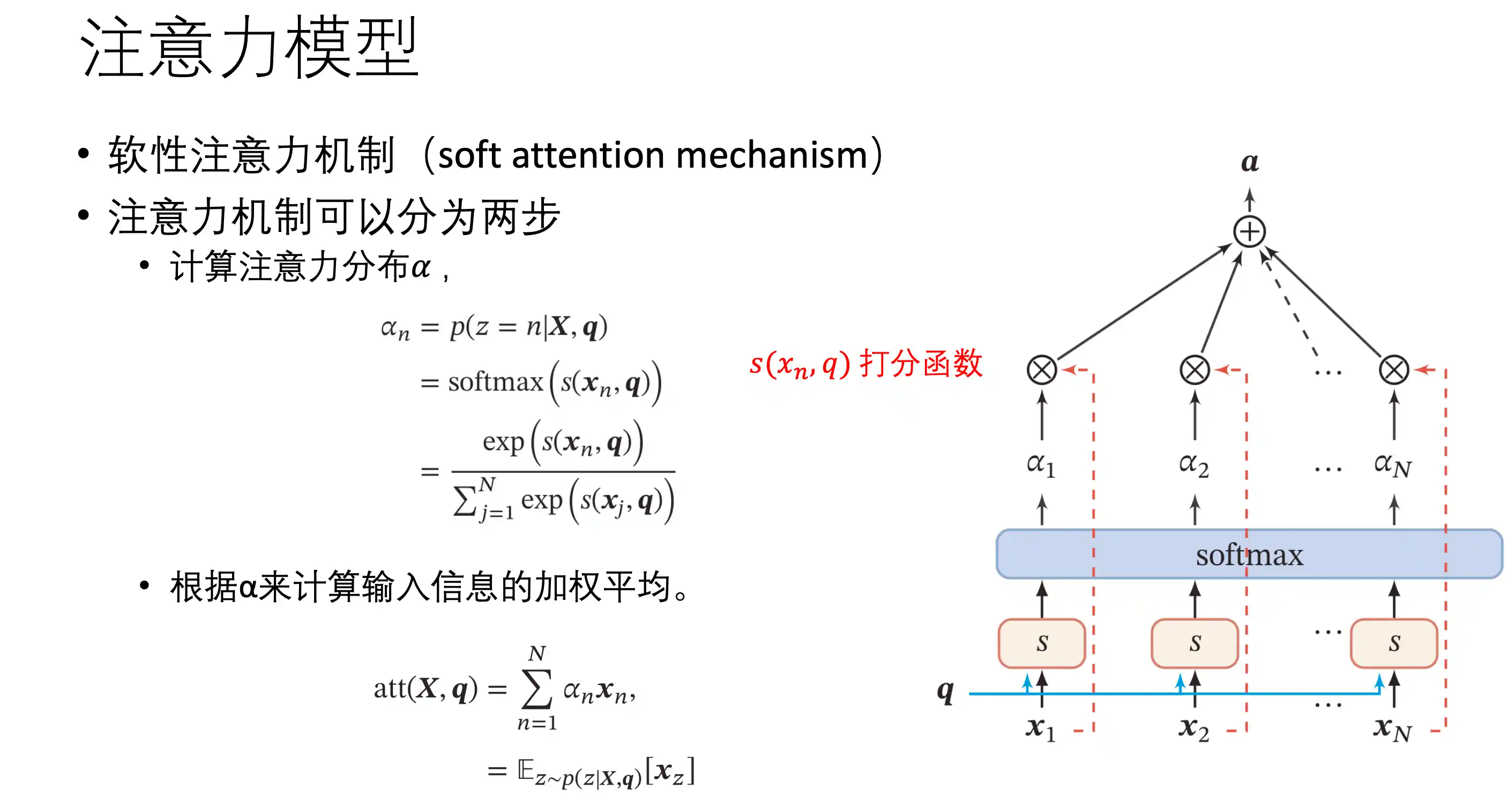
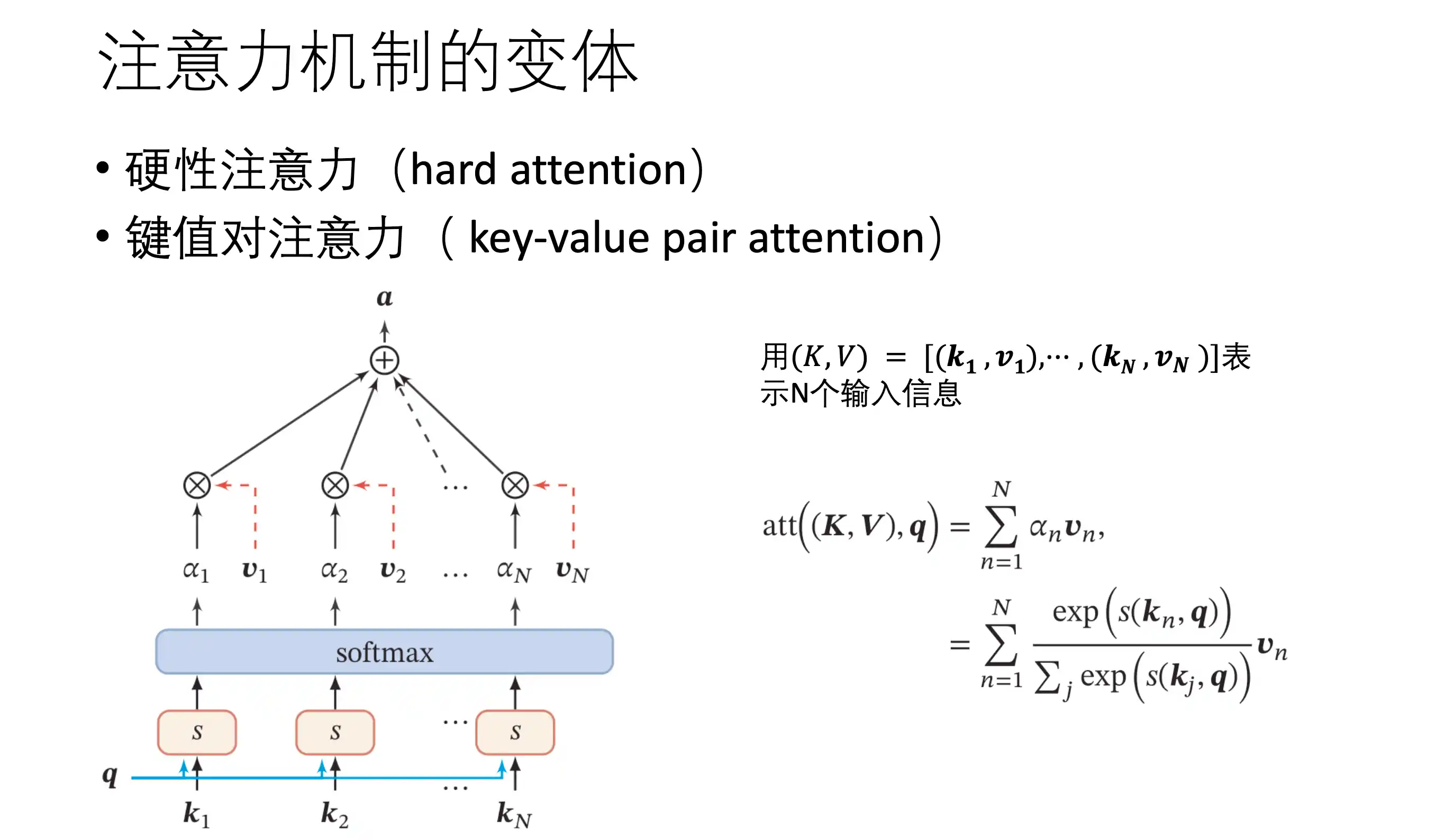
软性注意力机制 value 就是自己
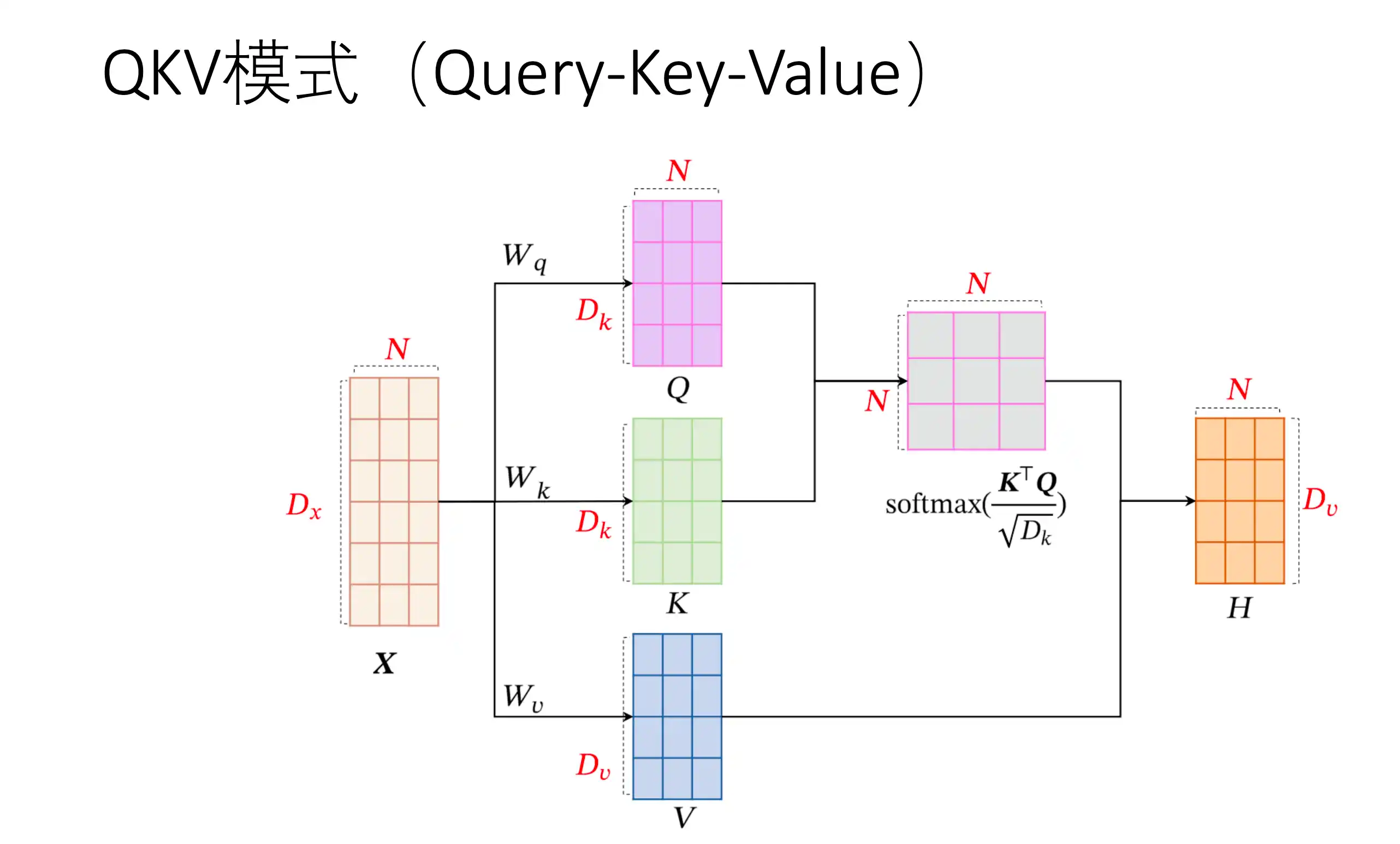
硬性注意力 QKV
多头注意力 多组查询Q KV是同一个
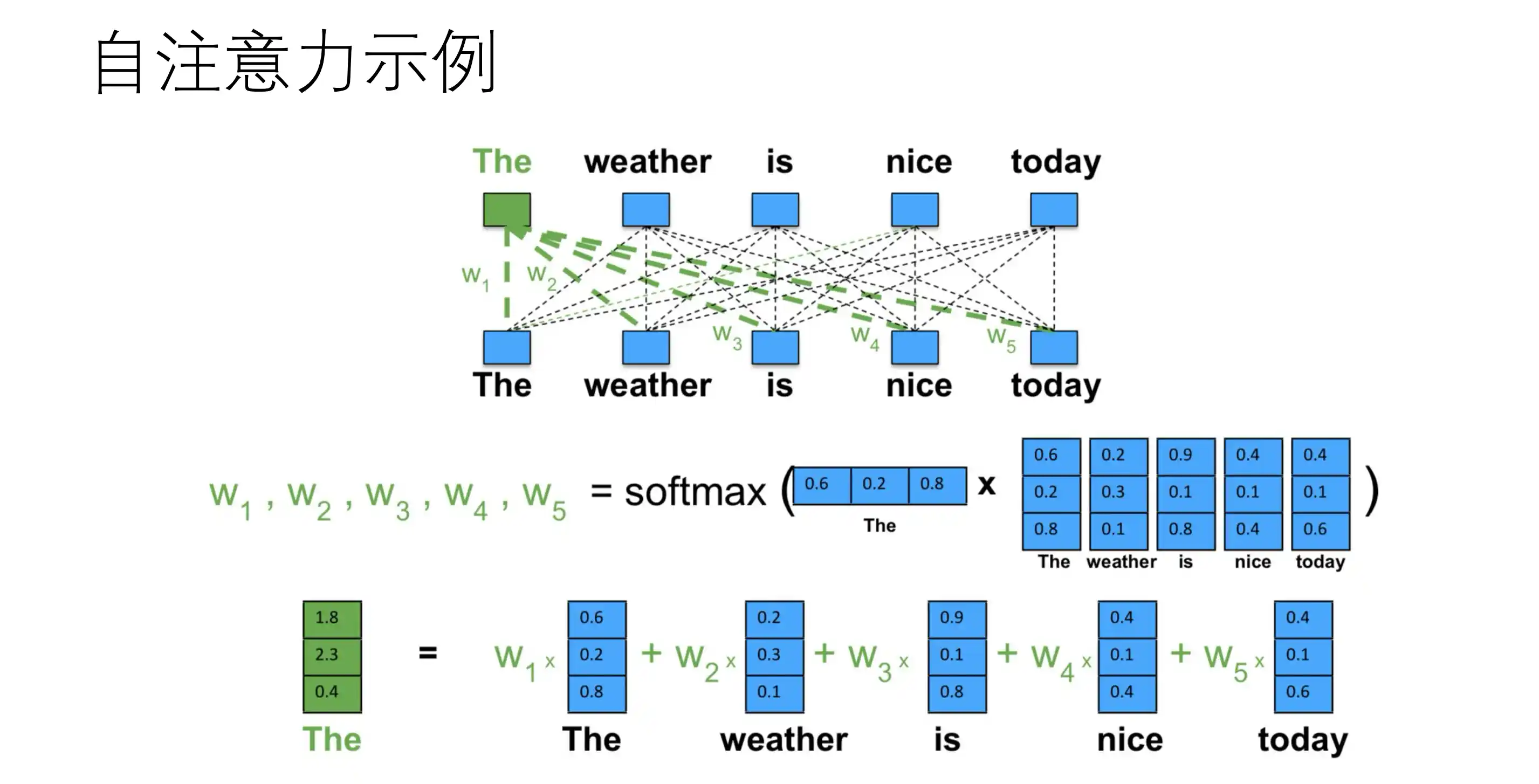
自注意力
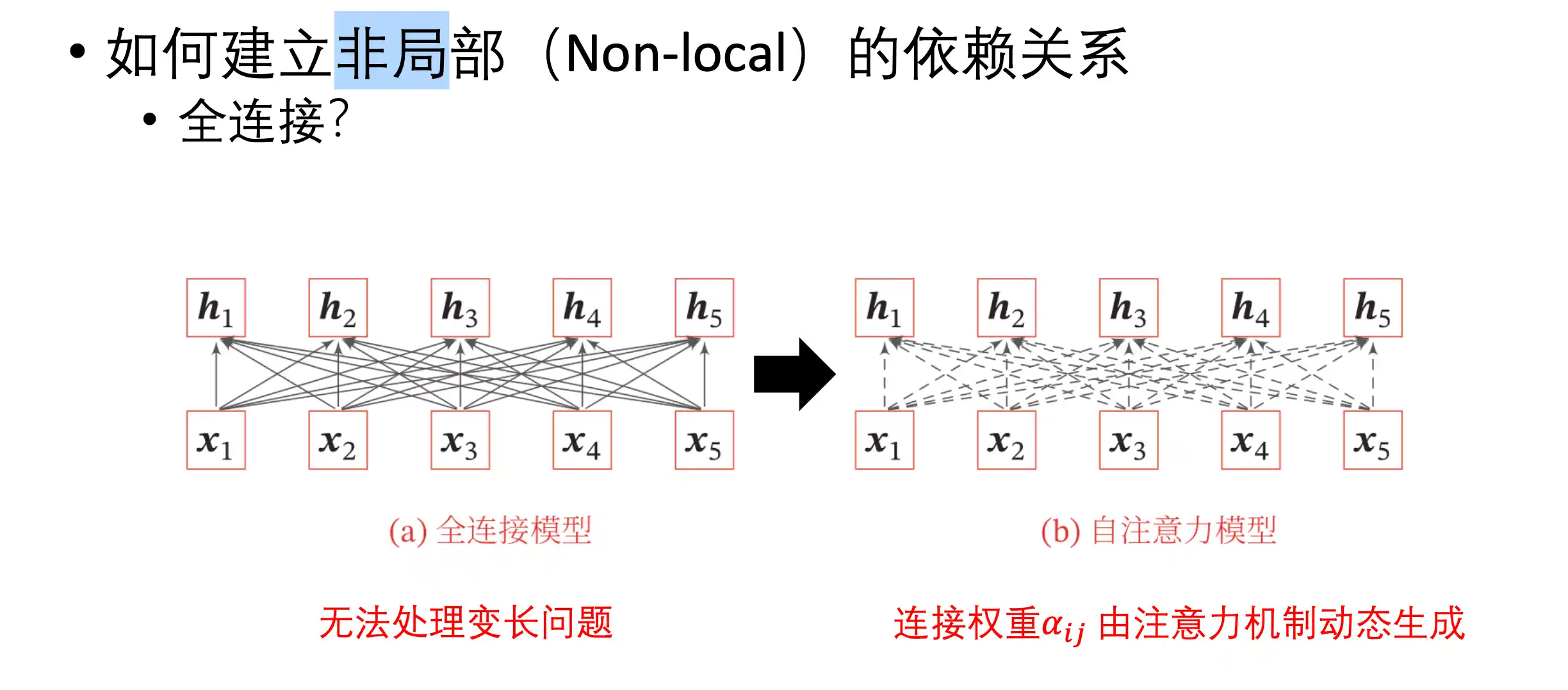
h2 只得到了 x1 x3 x2 的信息 卷积和循环只有local
全连接没法处理变长
自注意力示意图:
Transformer基本结构
自回归模型 为了建模一个变长序列出现的概率
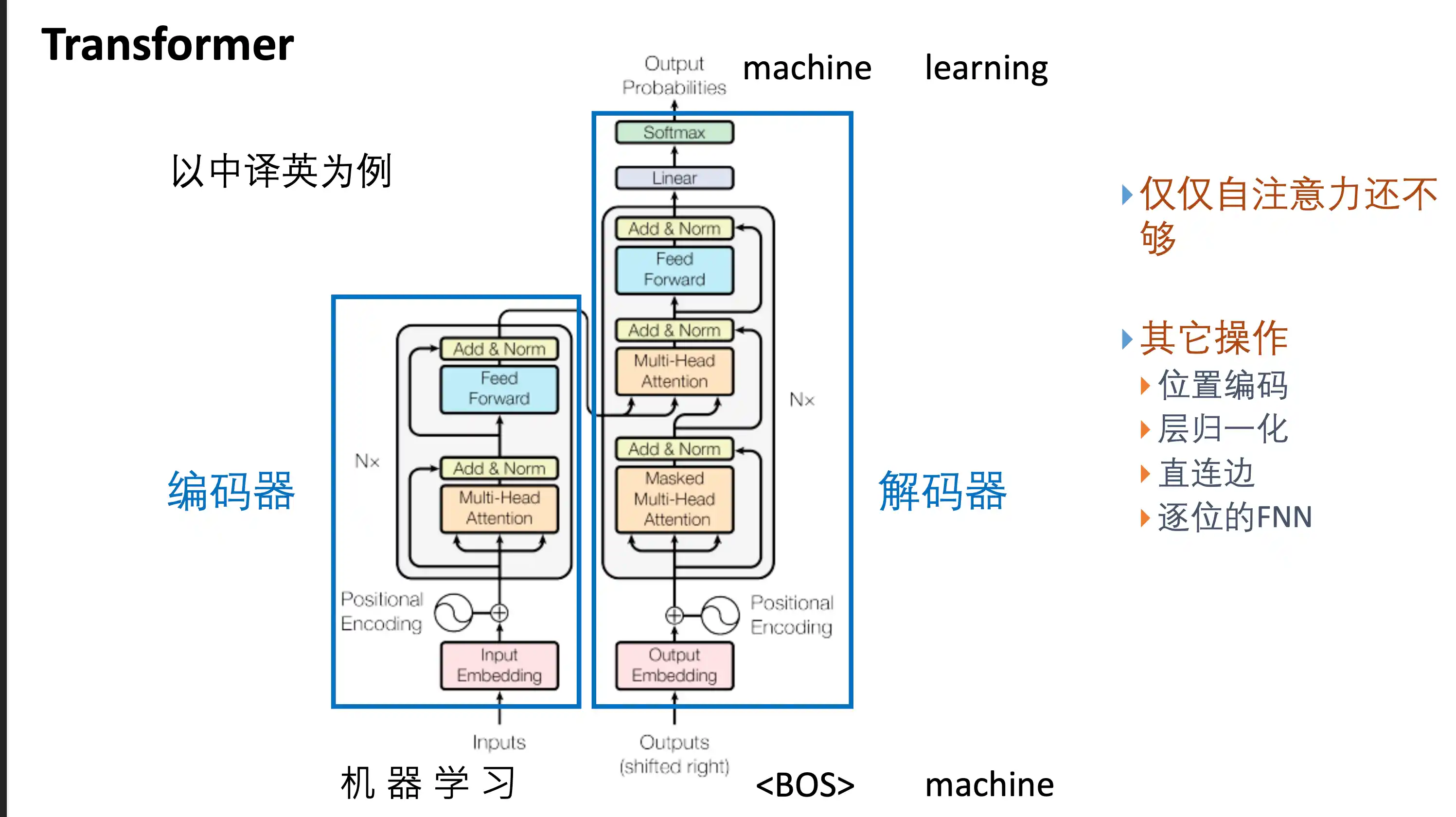
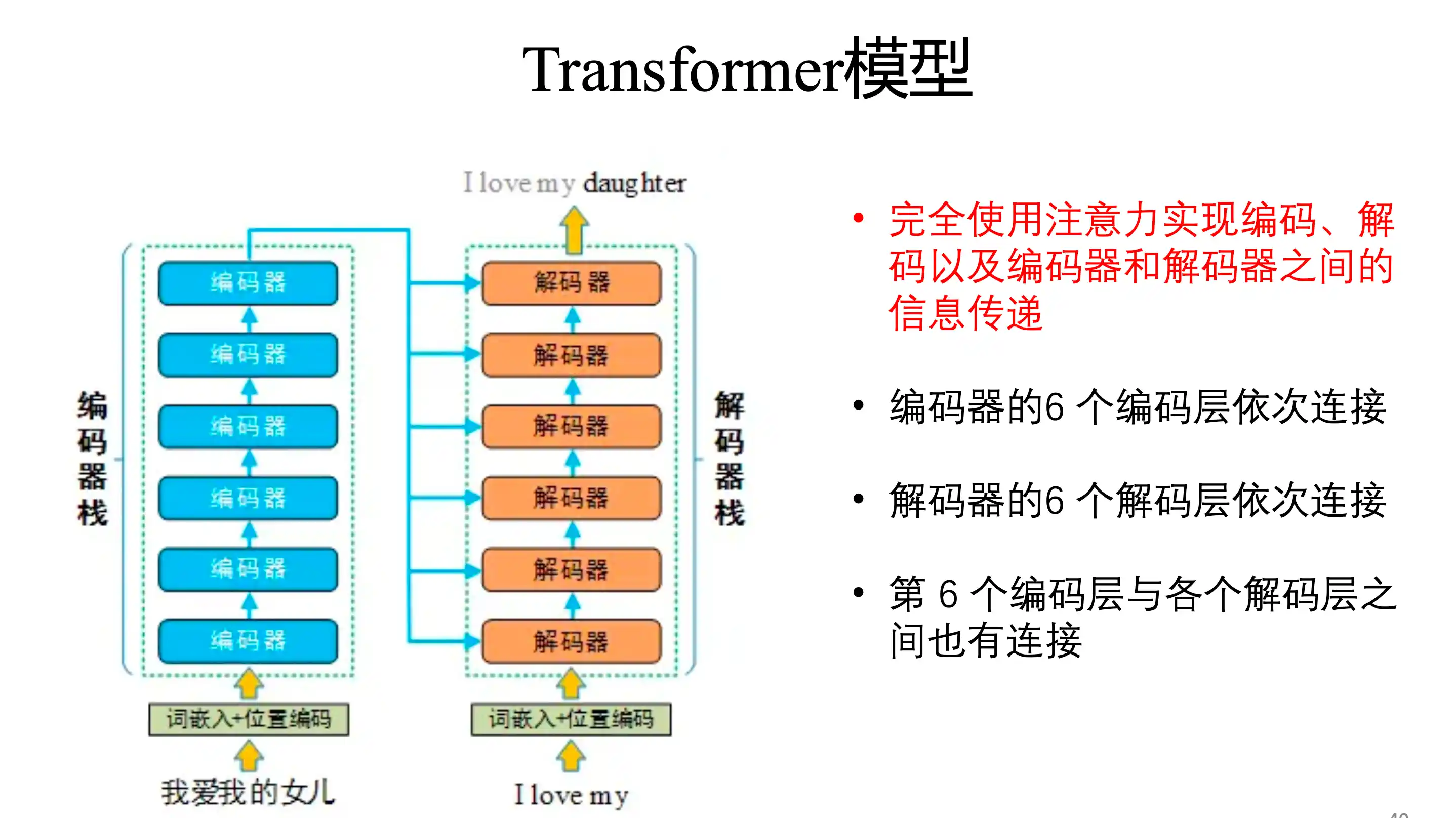
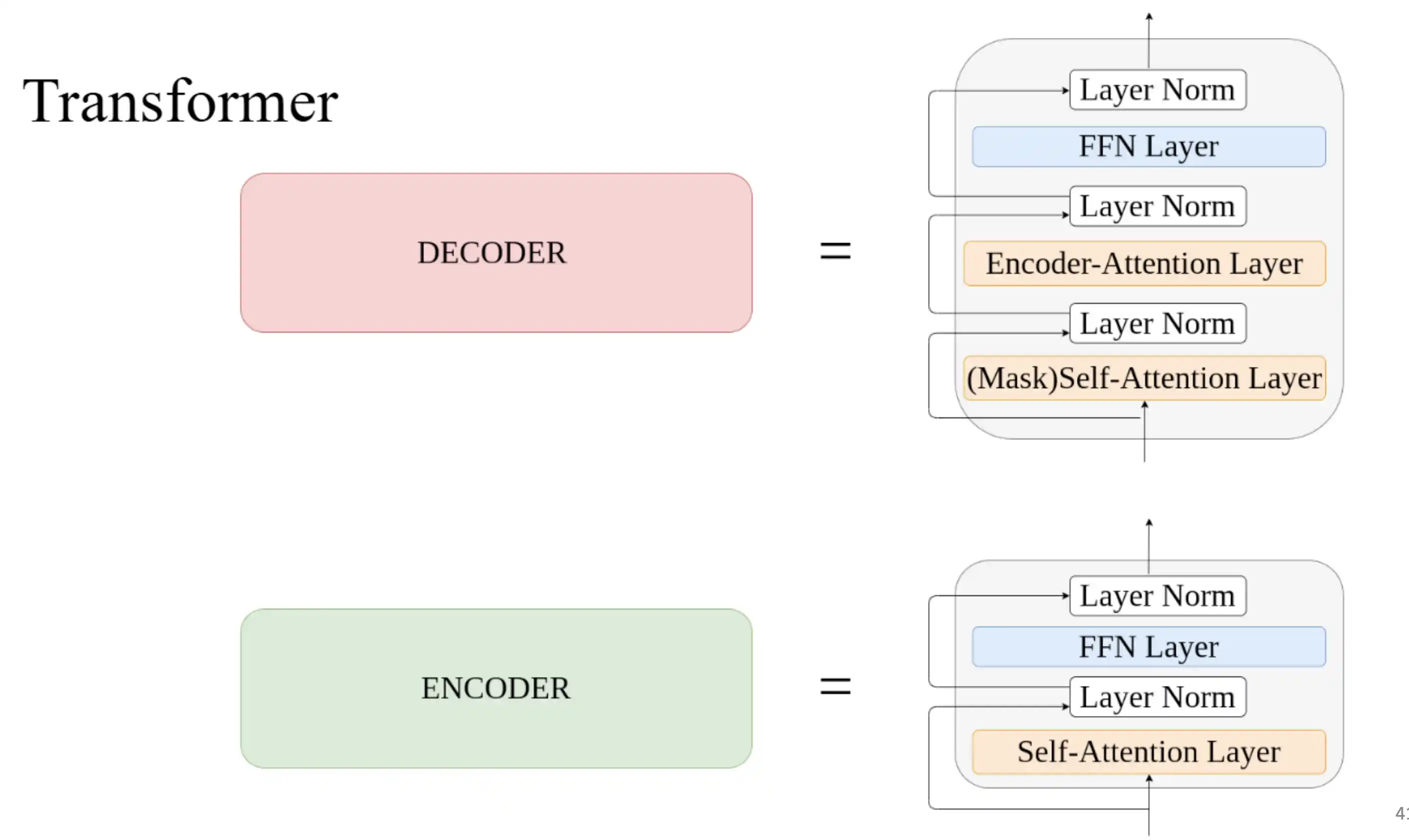
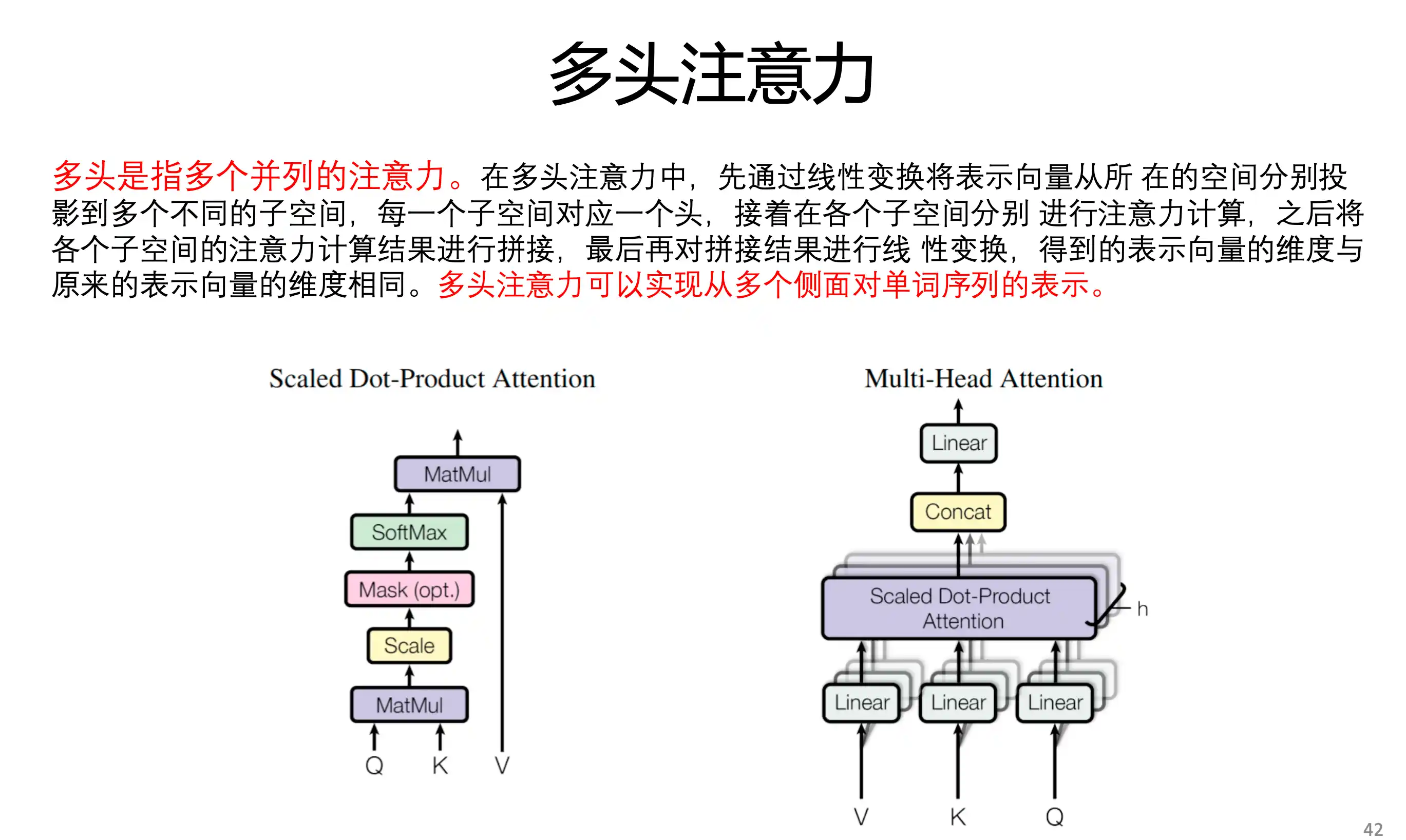


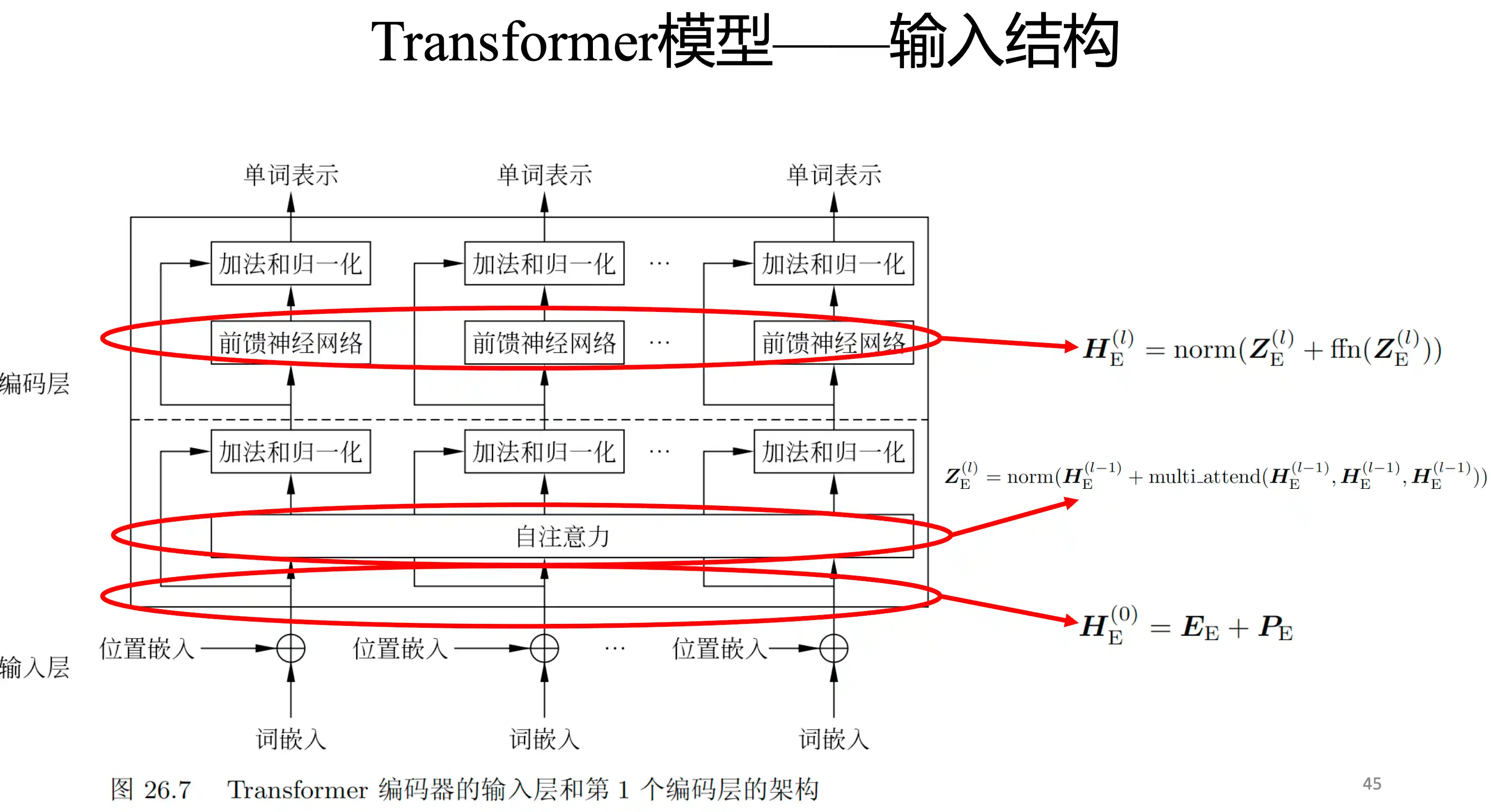
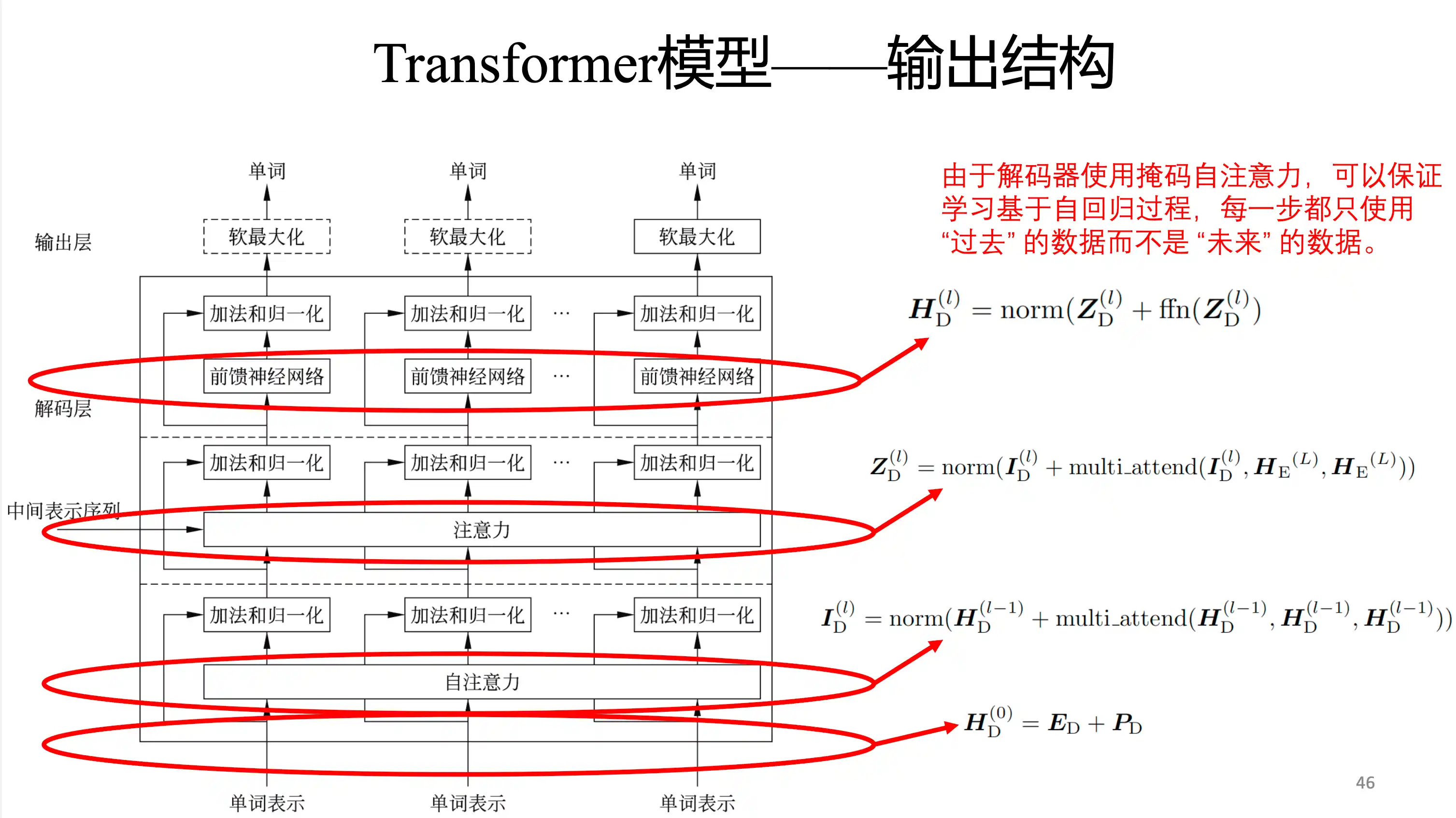
Transformer的特点

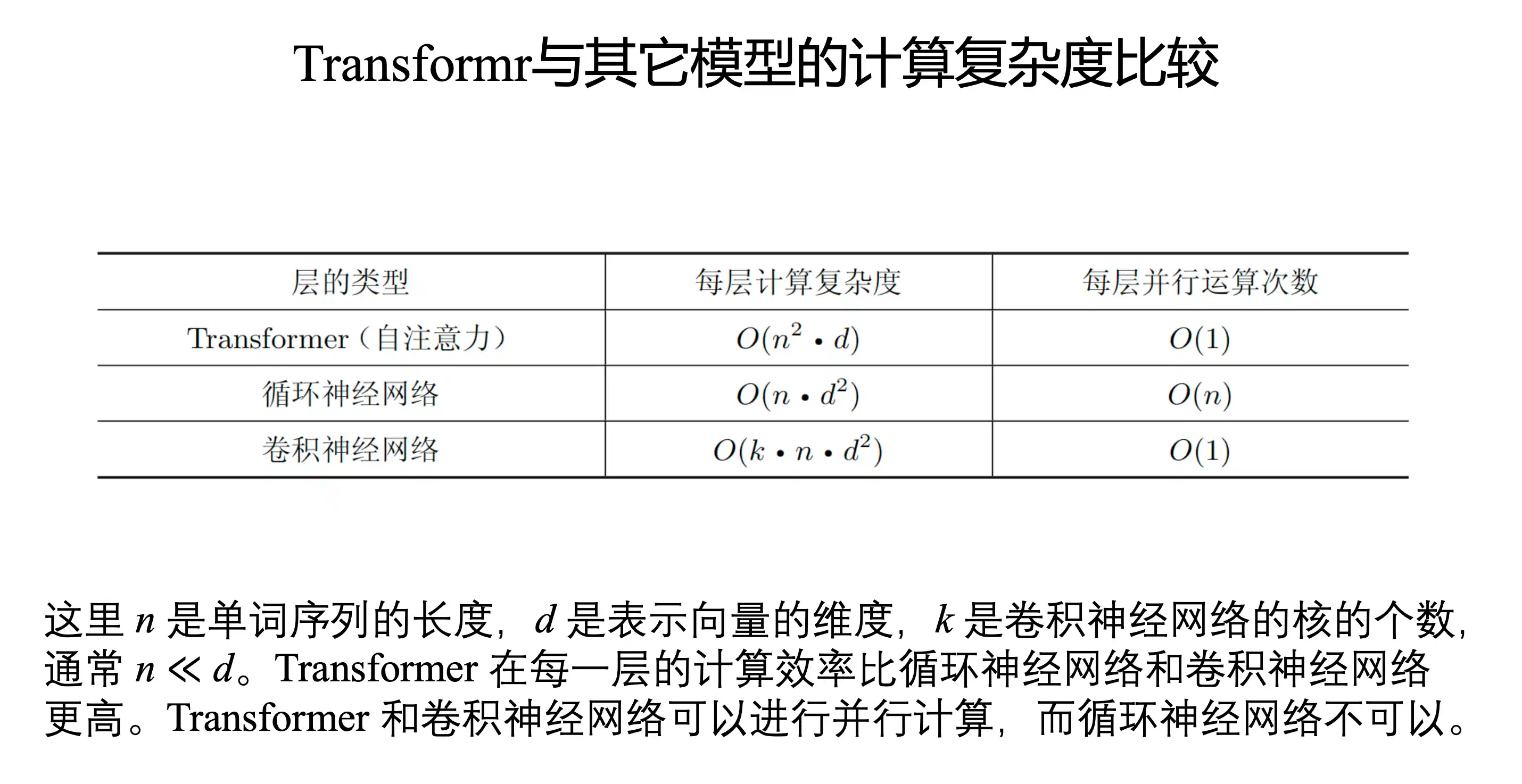
预训练语言模型BERT和GPT


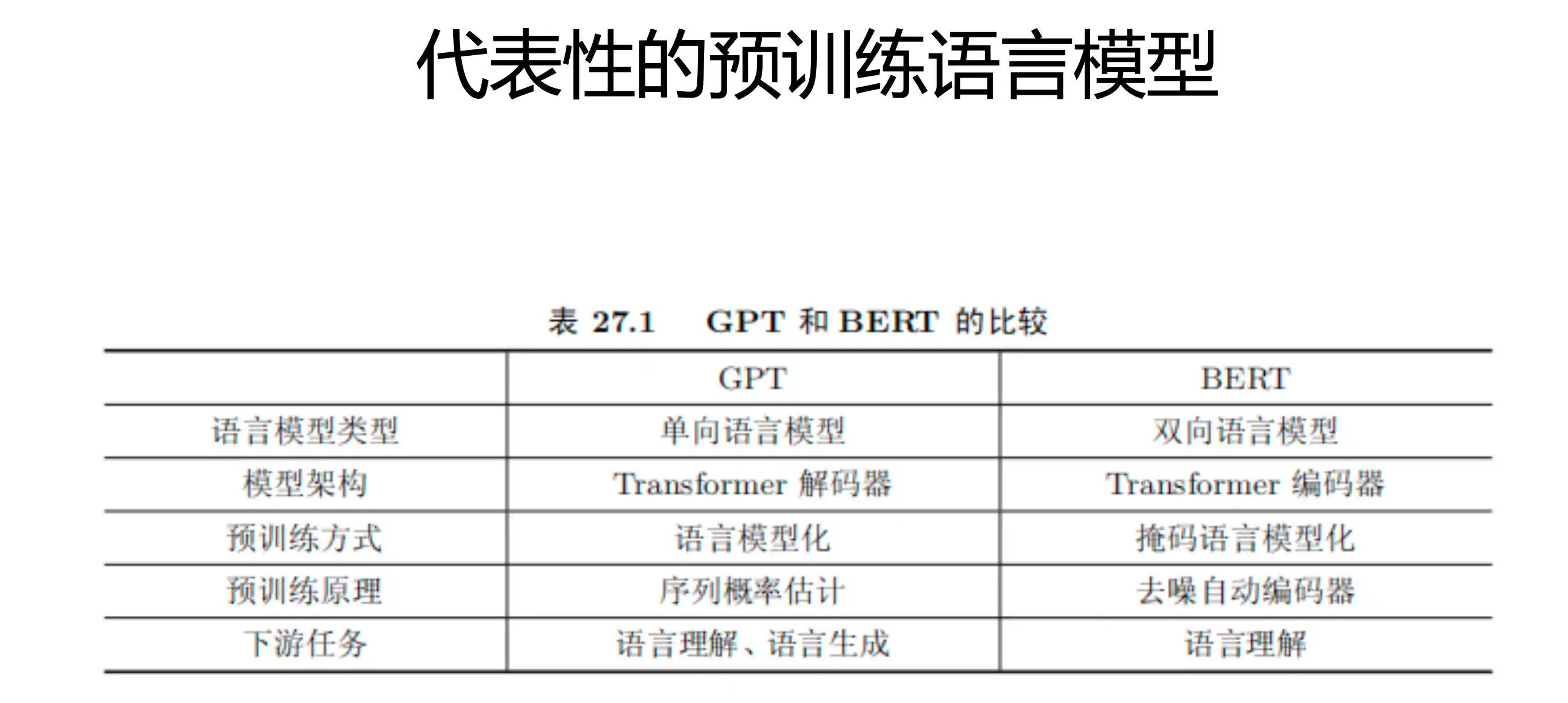
BERT模型
mask在中间的 不像 decoder 在一个地方 后面做mask
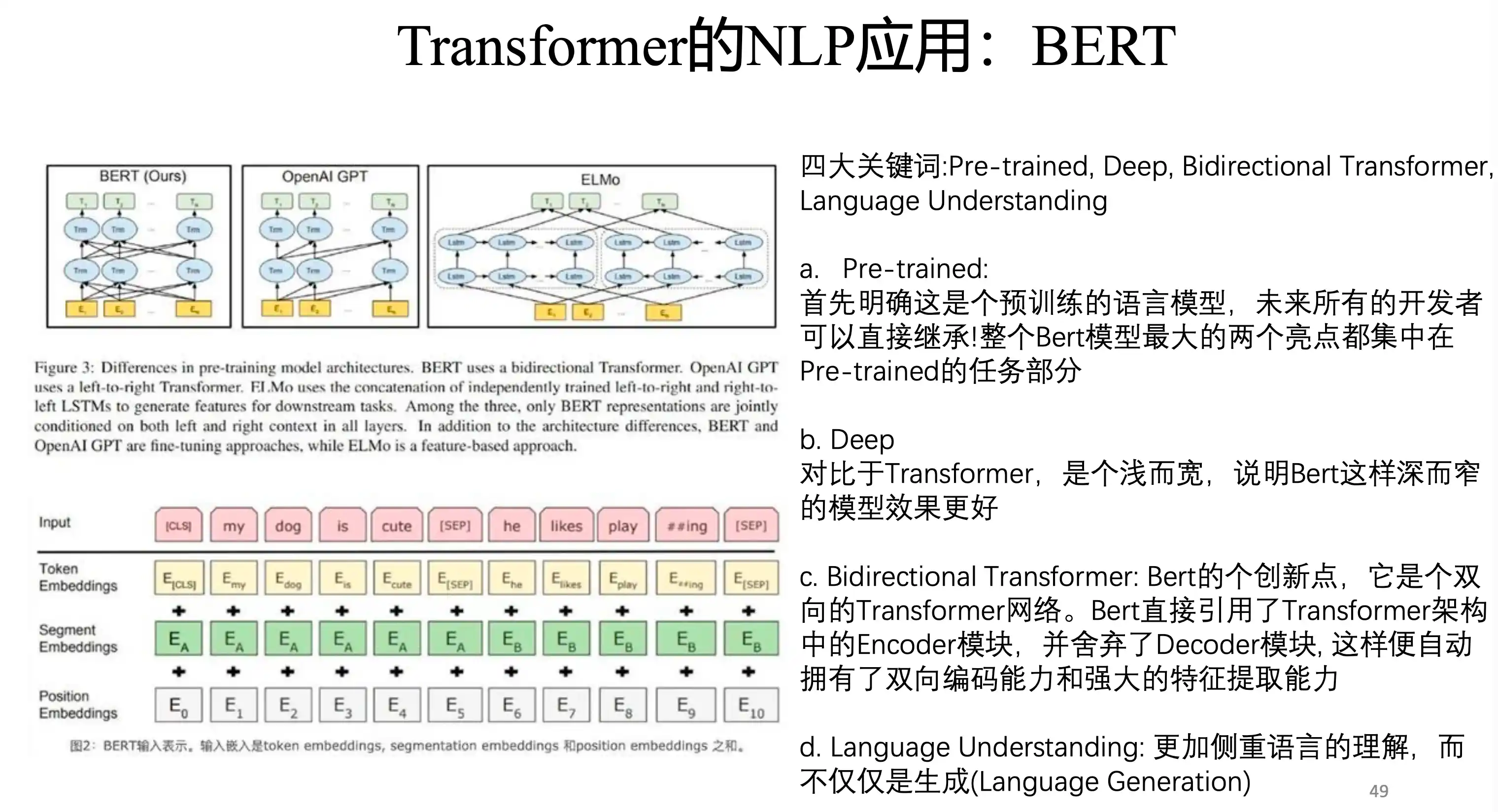

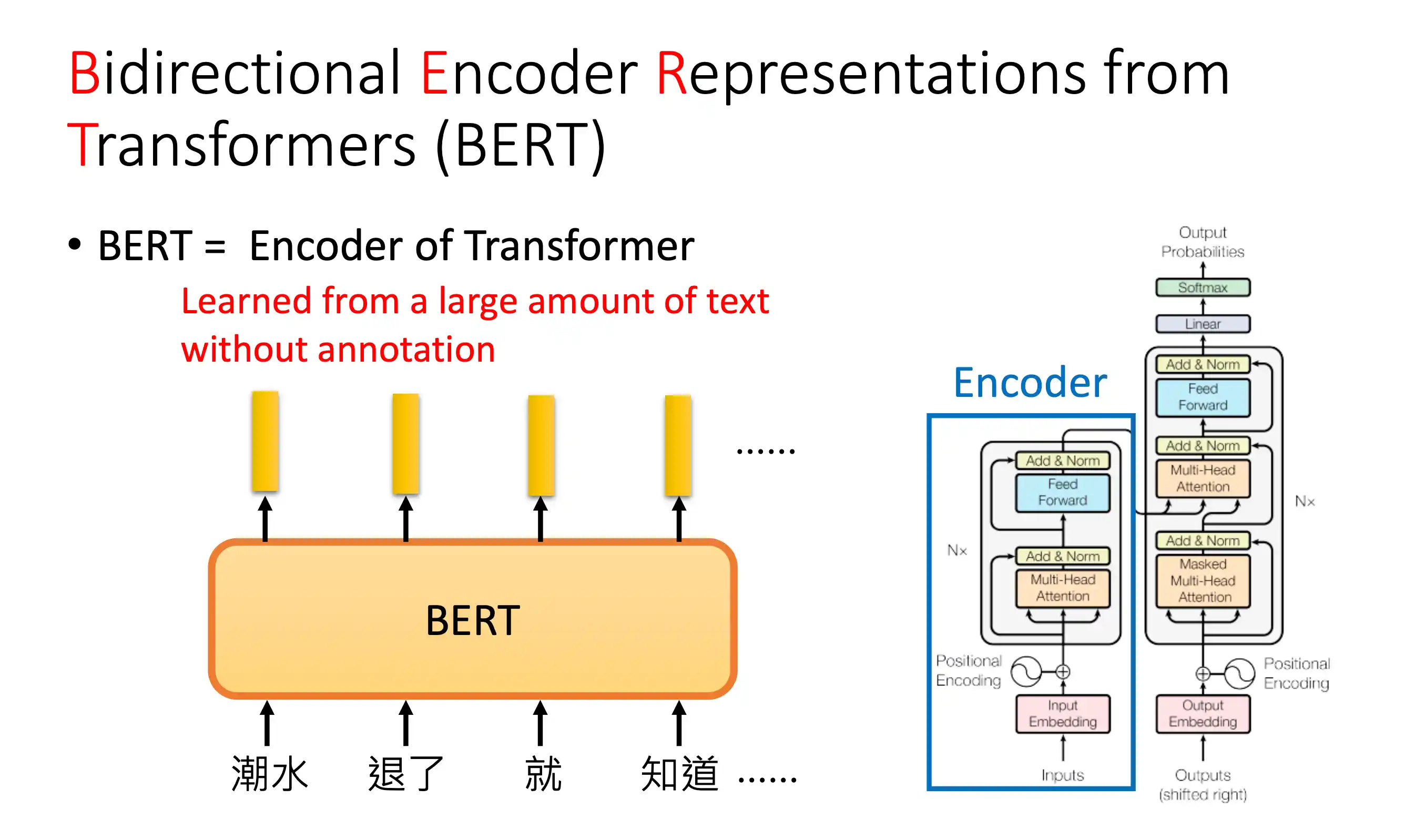
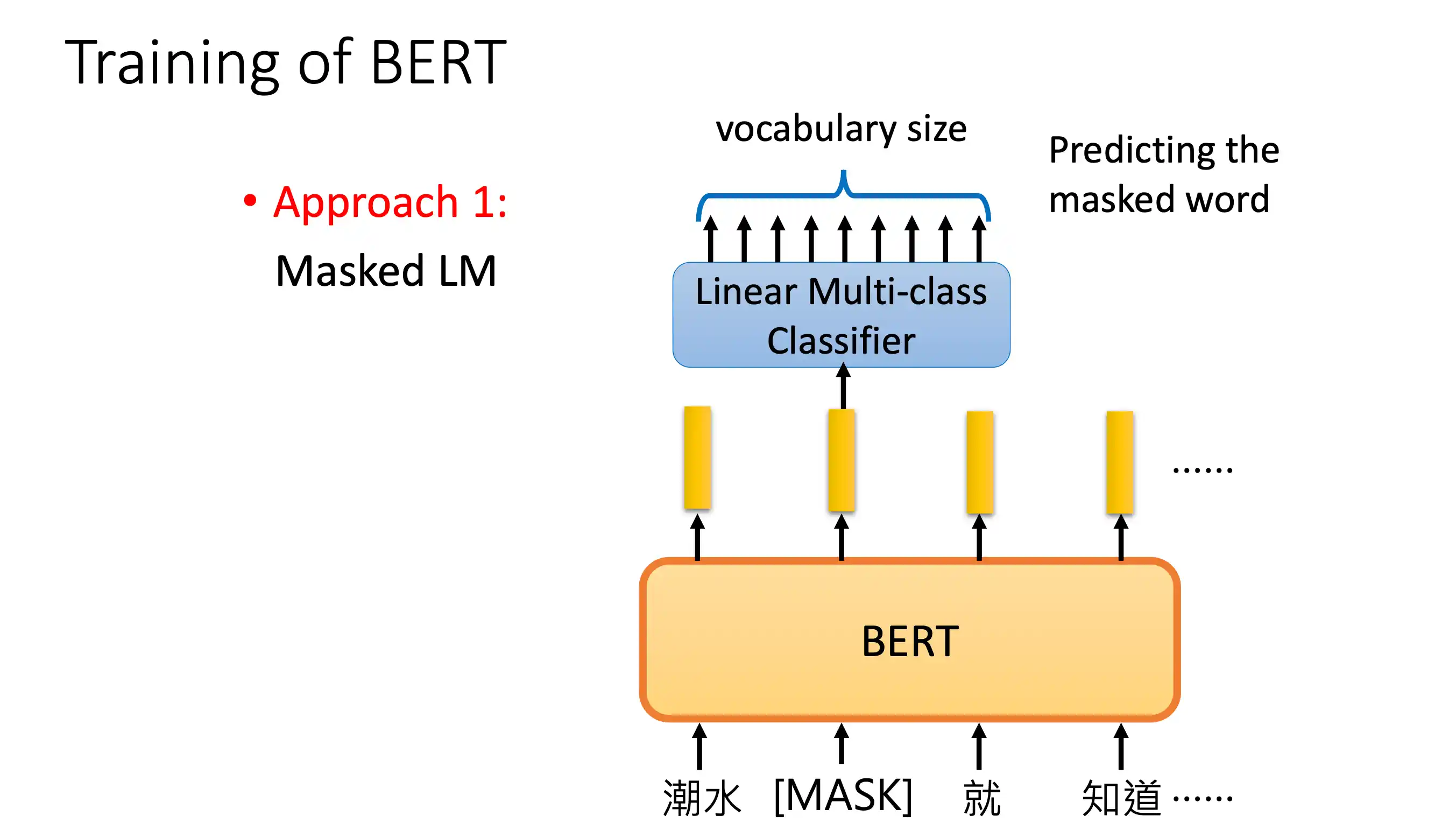
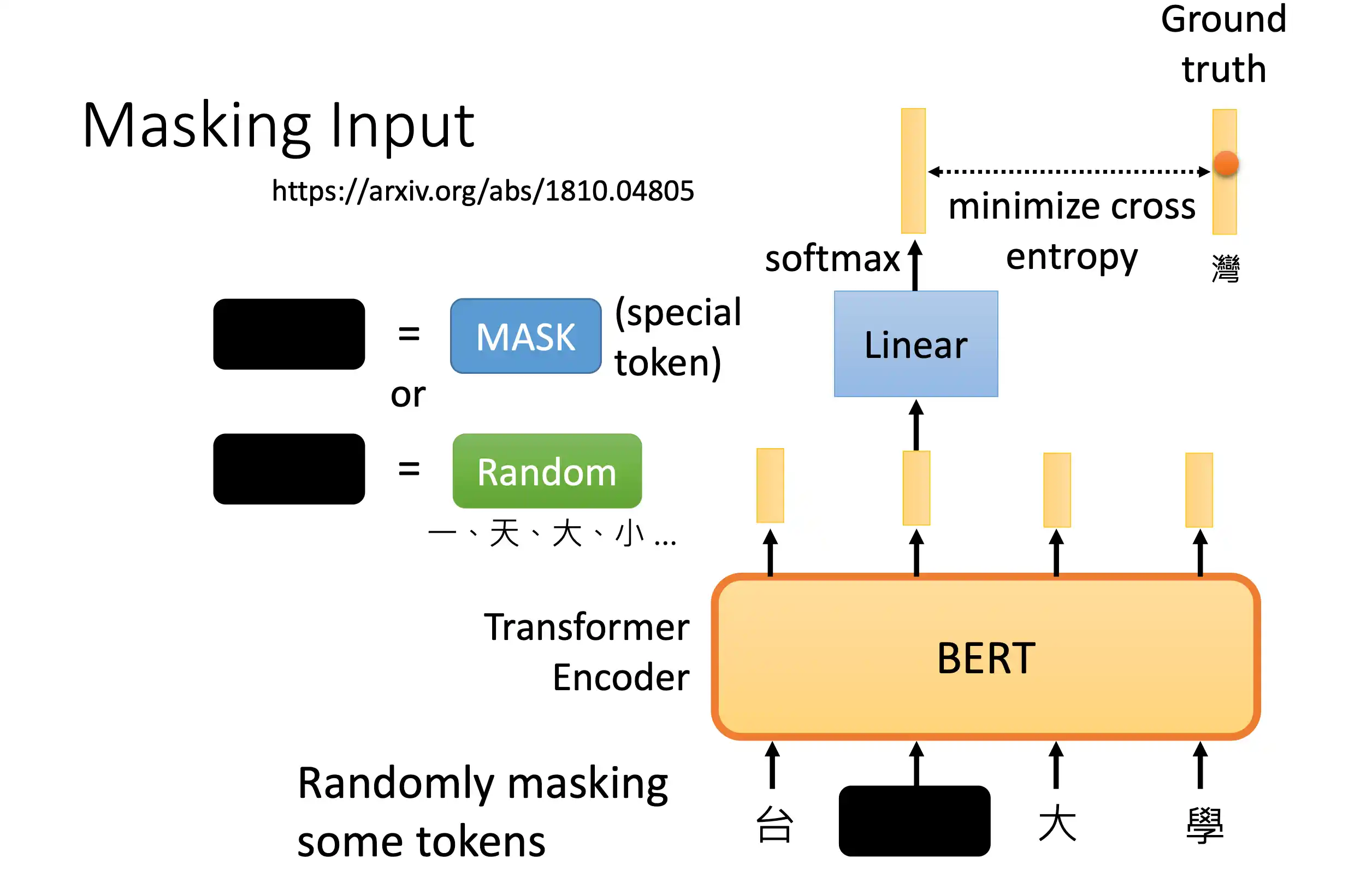
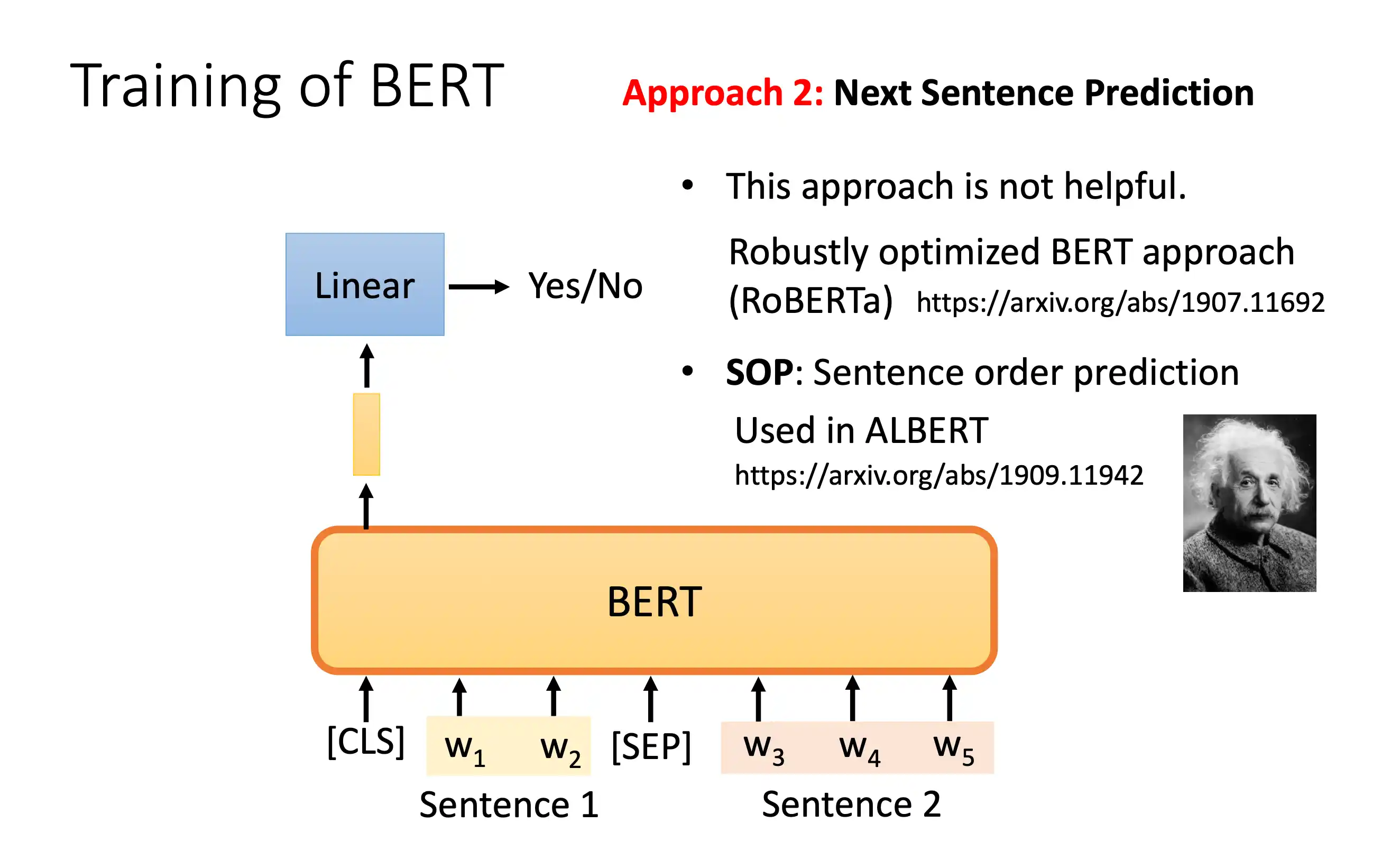
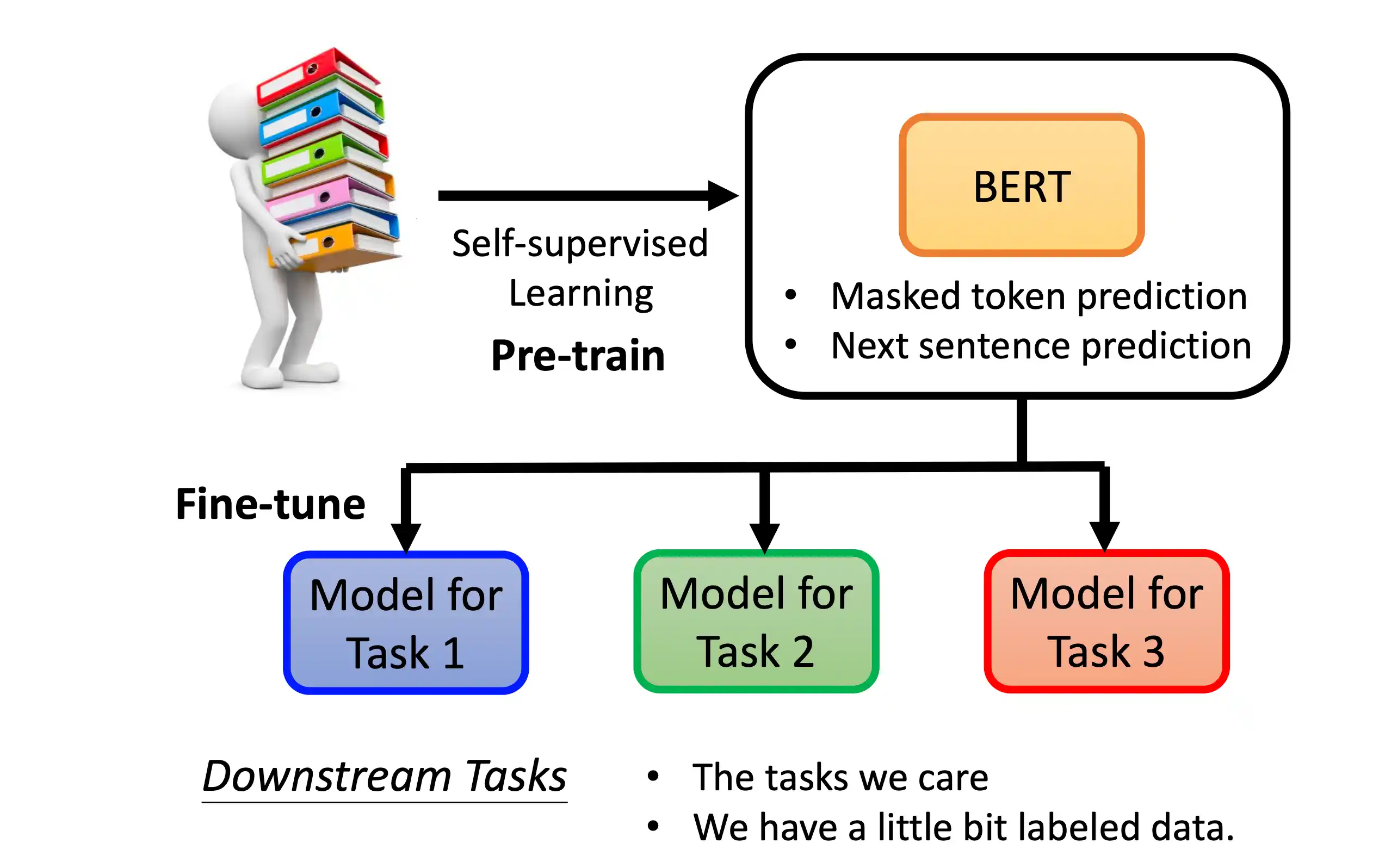
分类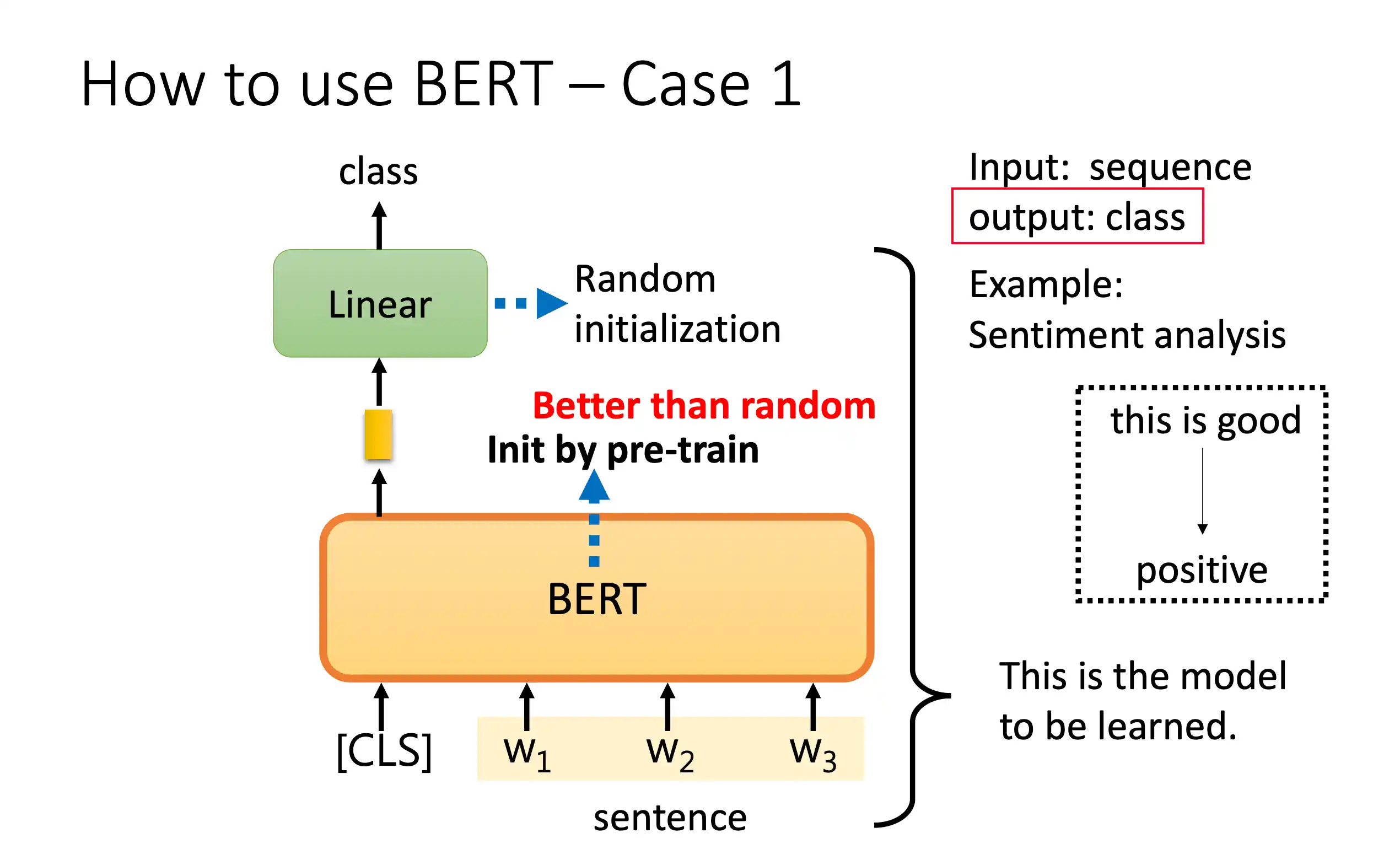
词性标注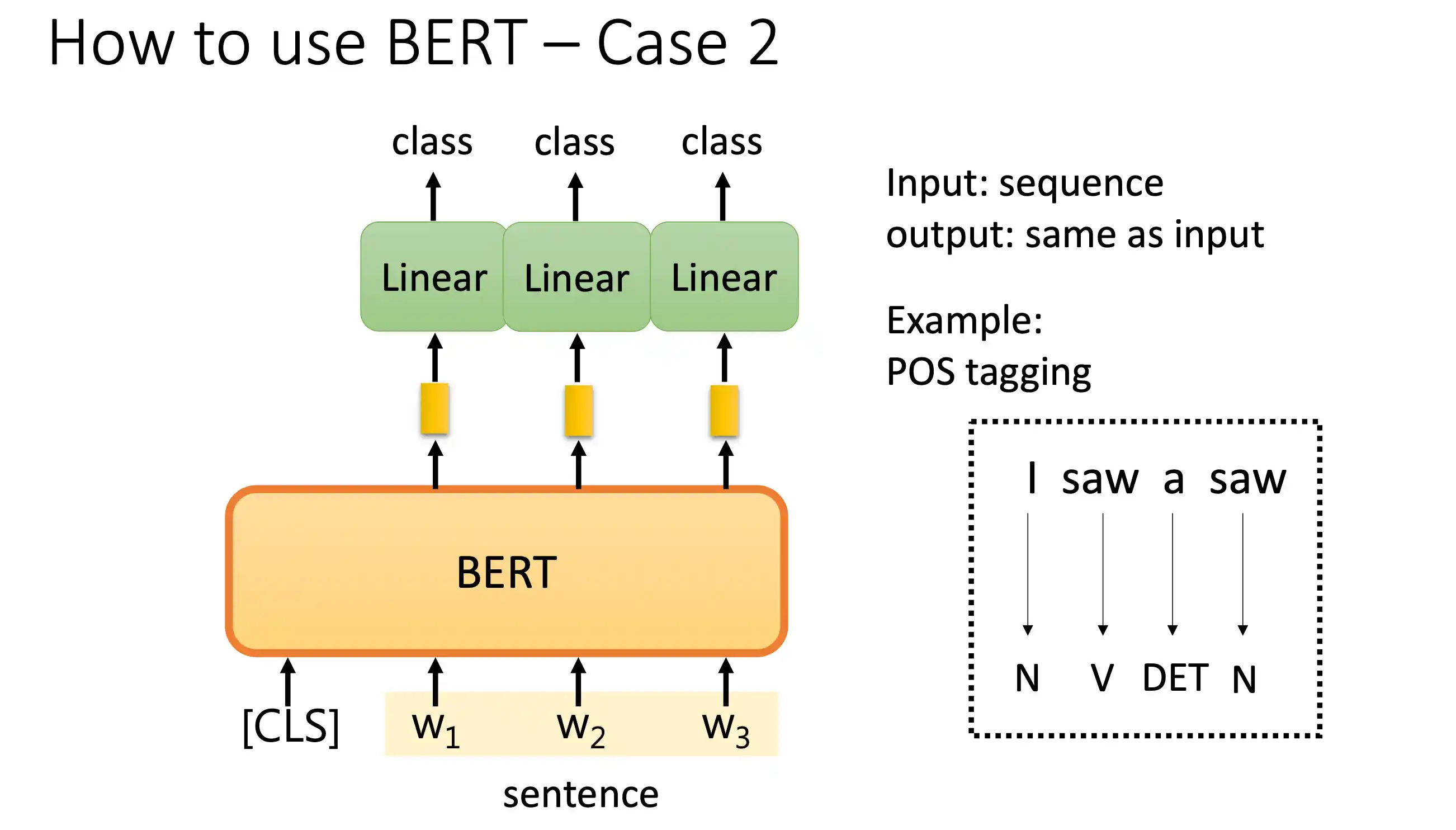
对对话分类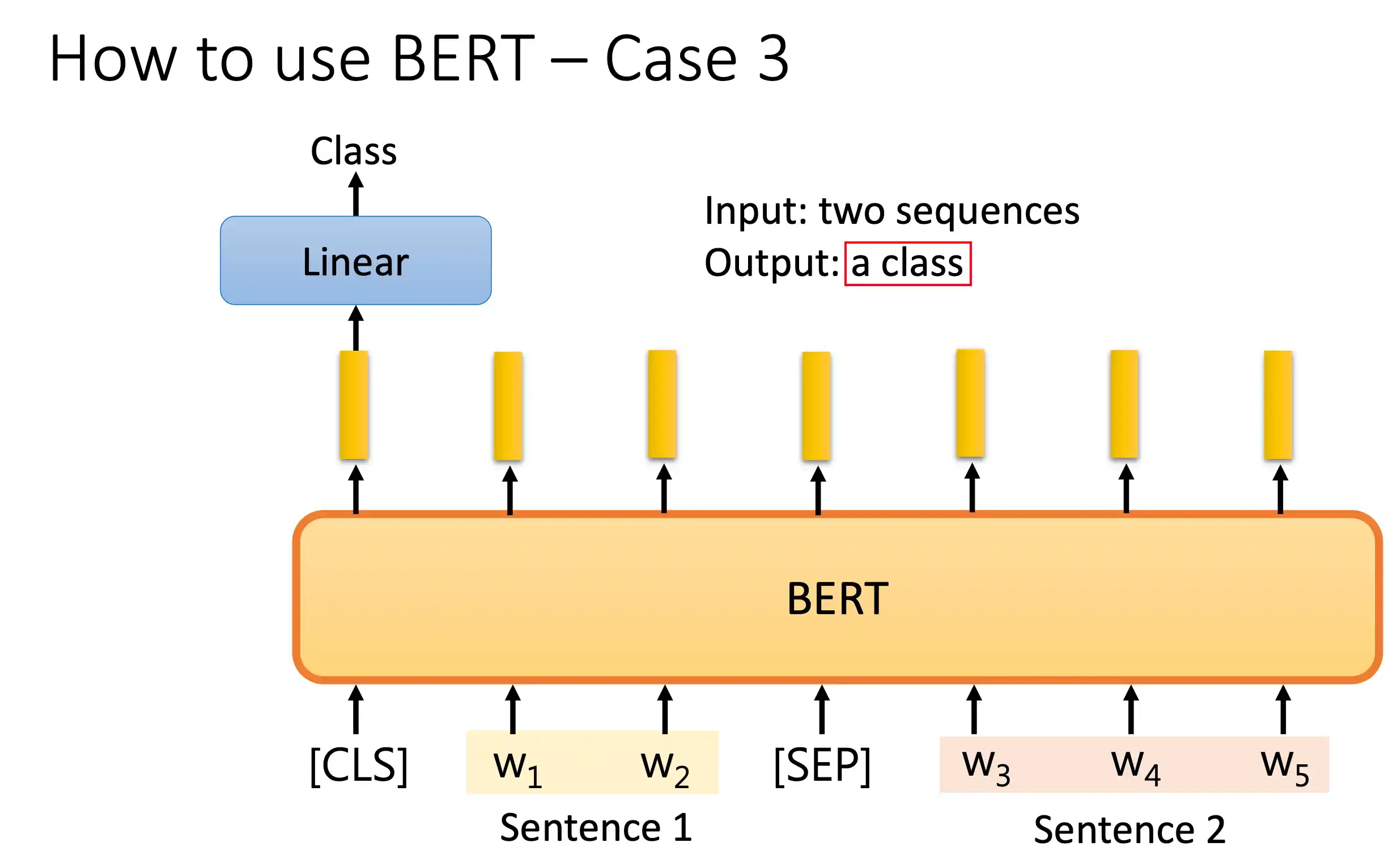
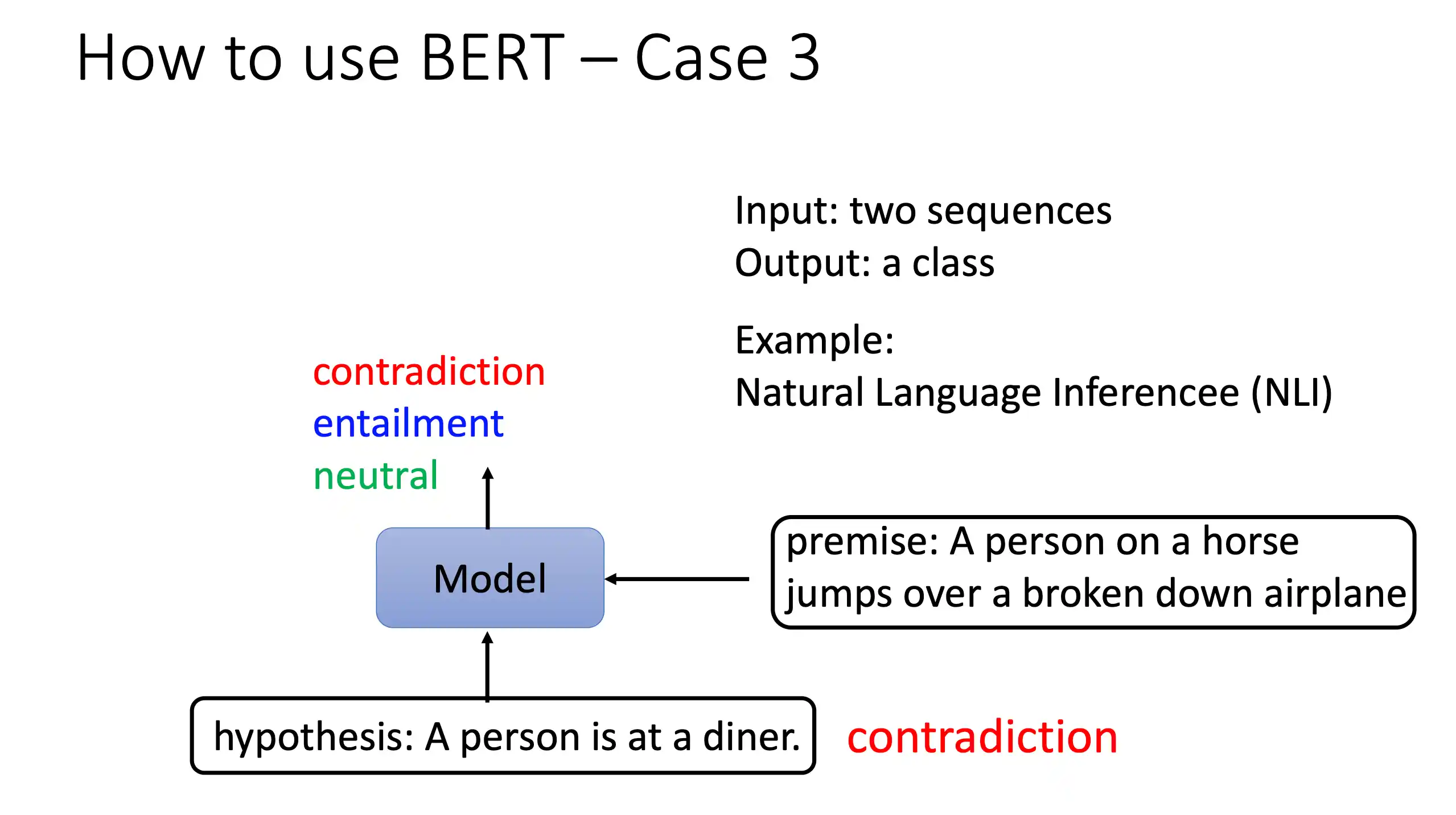
GPT
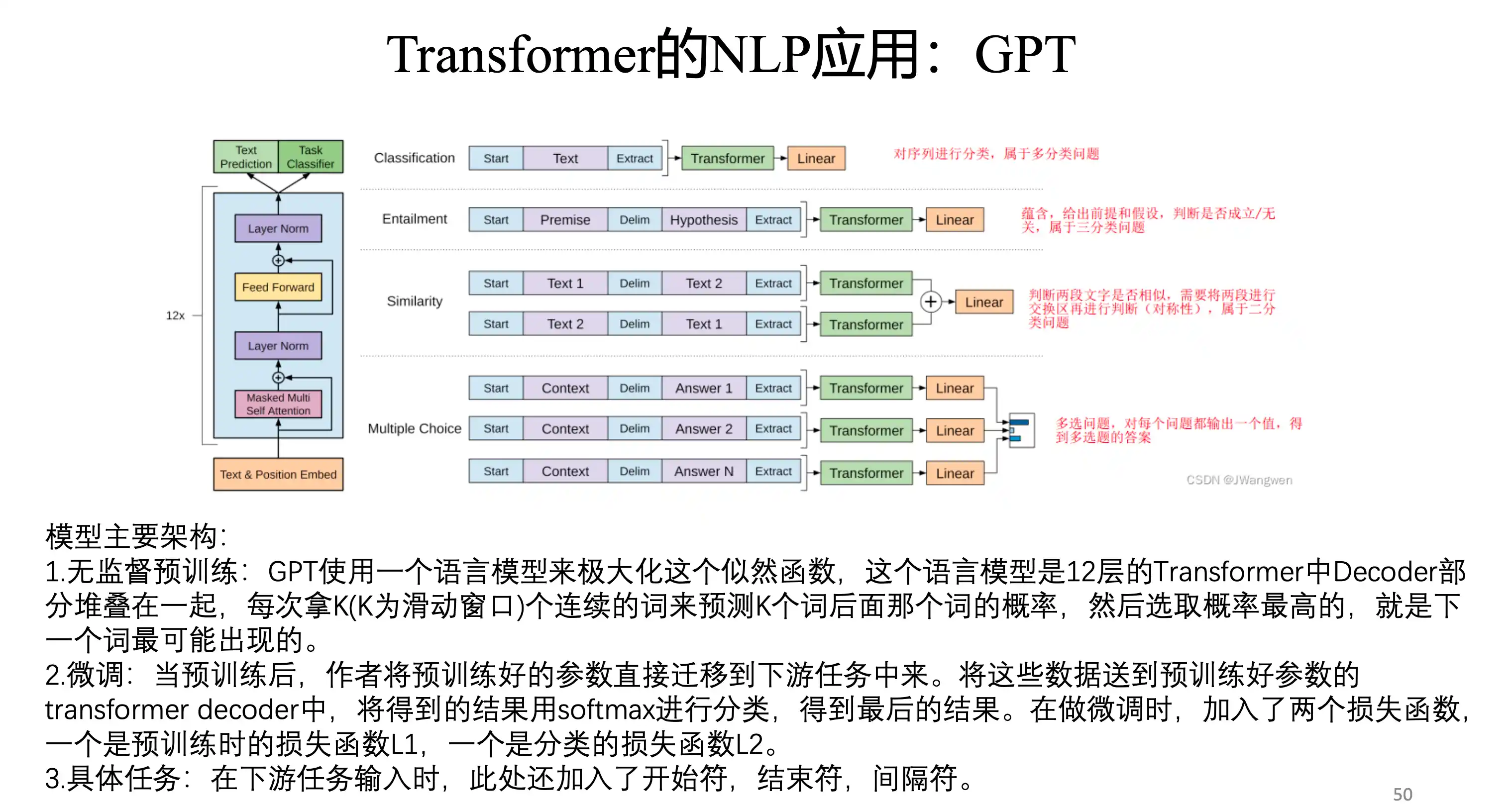

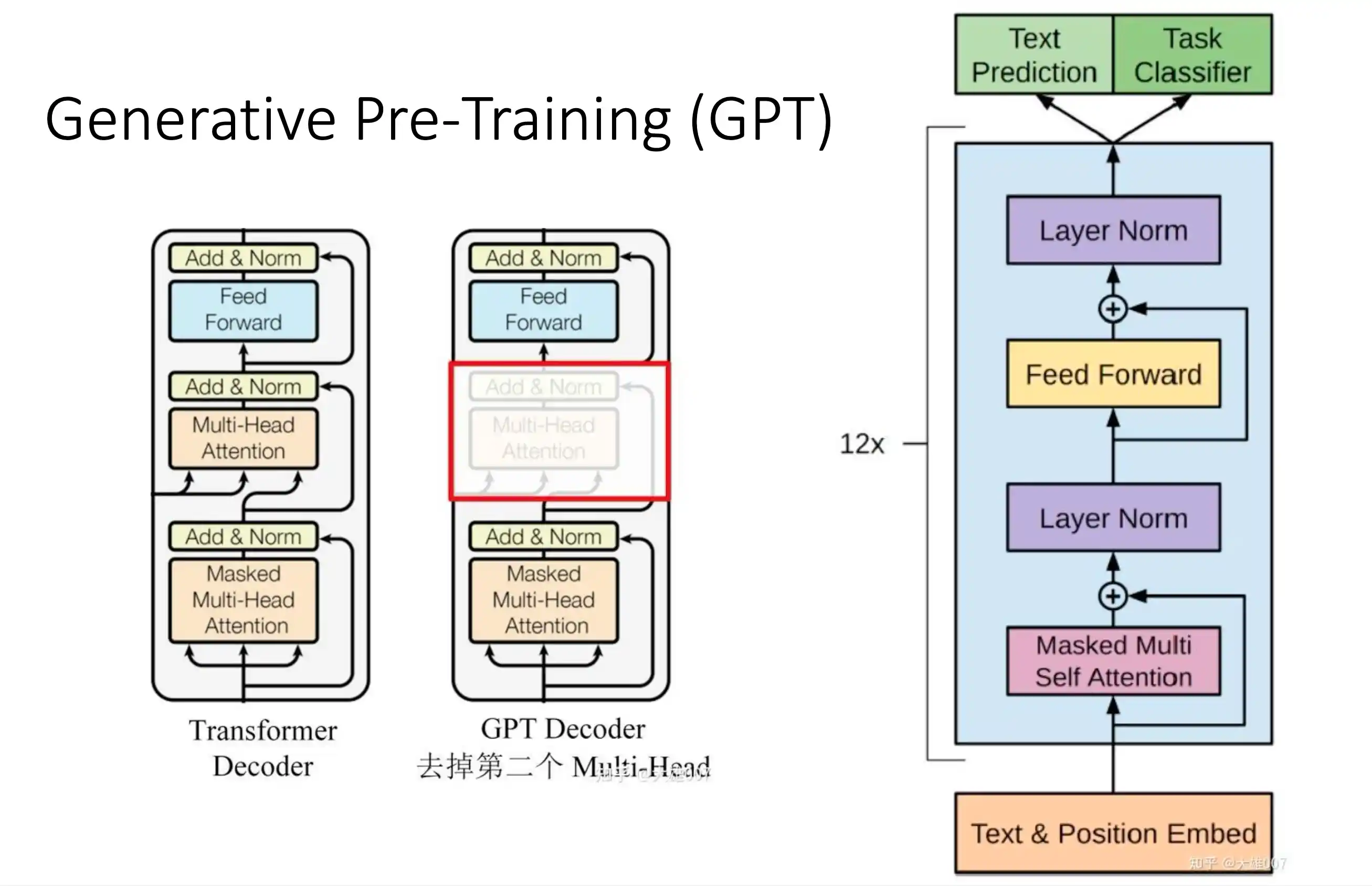
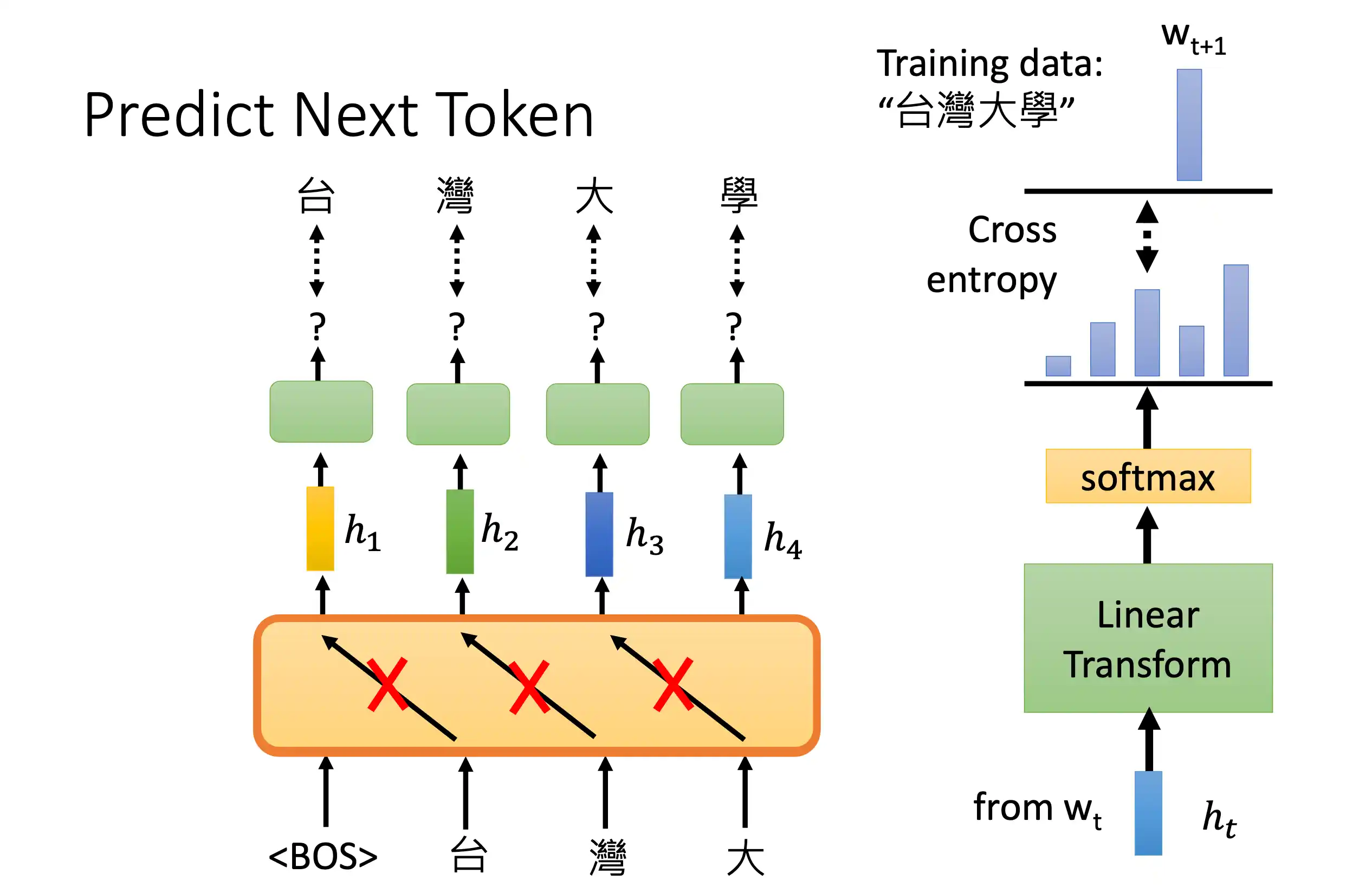

区别


第十章 强化学习
强化学习基本原理与构成
强化学习(Reinforcement Learning, 简称 RL)是机器学习的范式和方法论之一,用于描述和解决智能体(Agent)在与环境(Environment)的交互过程中通过学习策略(Policy)以达成奖励或回报(Reward)最大化或实现特定目标的问题。
强化学习和其他机器学习范式不同的的原因:
没有 做loss的步骤 非及时反馈
奖励:

例如:
乘坐直升机进⾏特技⻜⾏操作
• 因遵循期望轨迹获得正奖励
• 因坠毁获得负奖励
在西洋双陆棋比赛中击败世界冠军
• +/− 因赢得/输掉⼀局比赛获得的正负奖励
让类人机器人⾏⾛
• 向前移动给予正奖励
• 摔倒给予负奖励
决策序列
智能体与环境的交互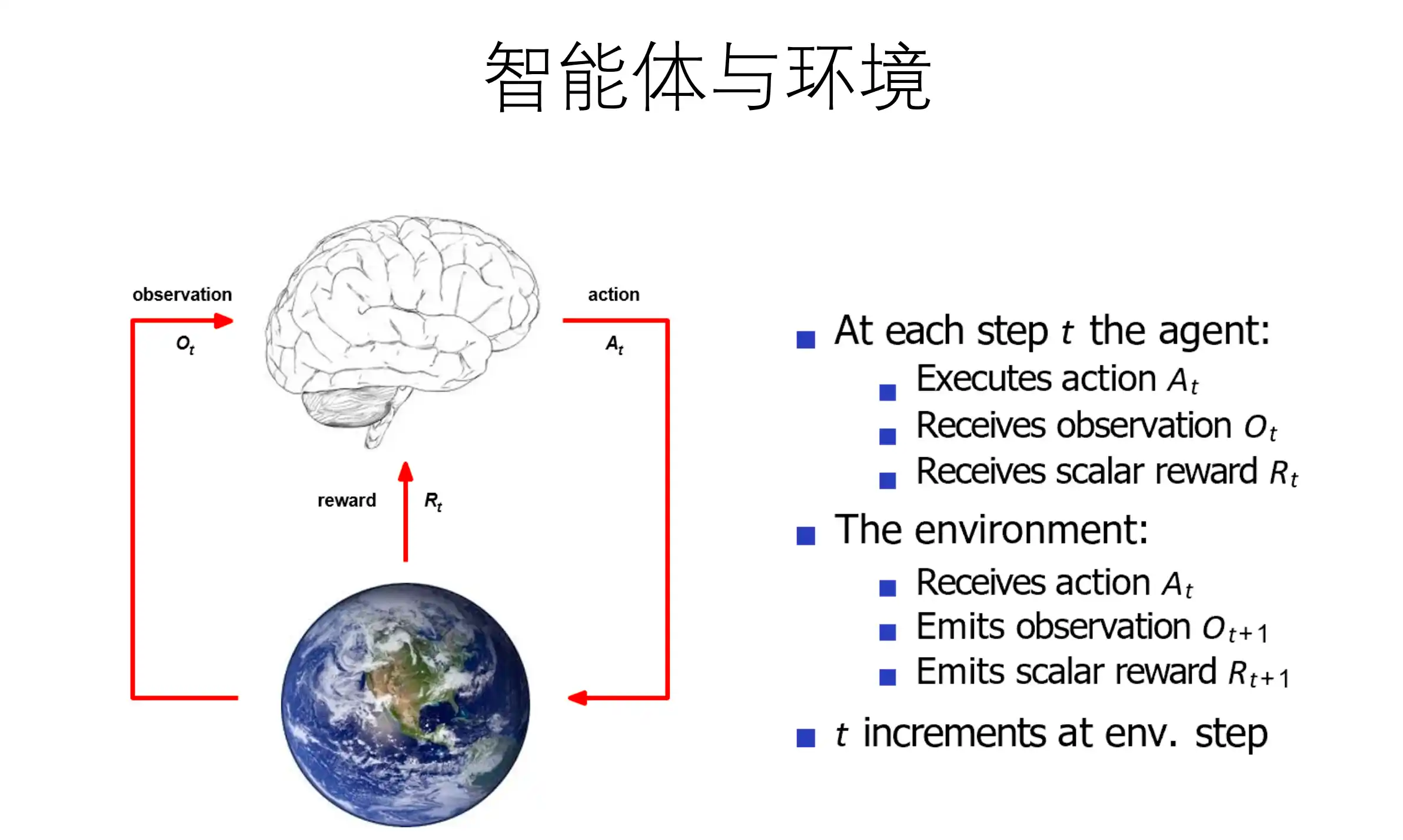
历史与状态
信息状态
智能体的构成
主要组件
- 策略

- 价值函数

- 模型

智能体分类


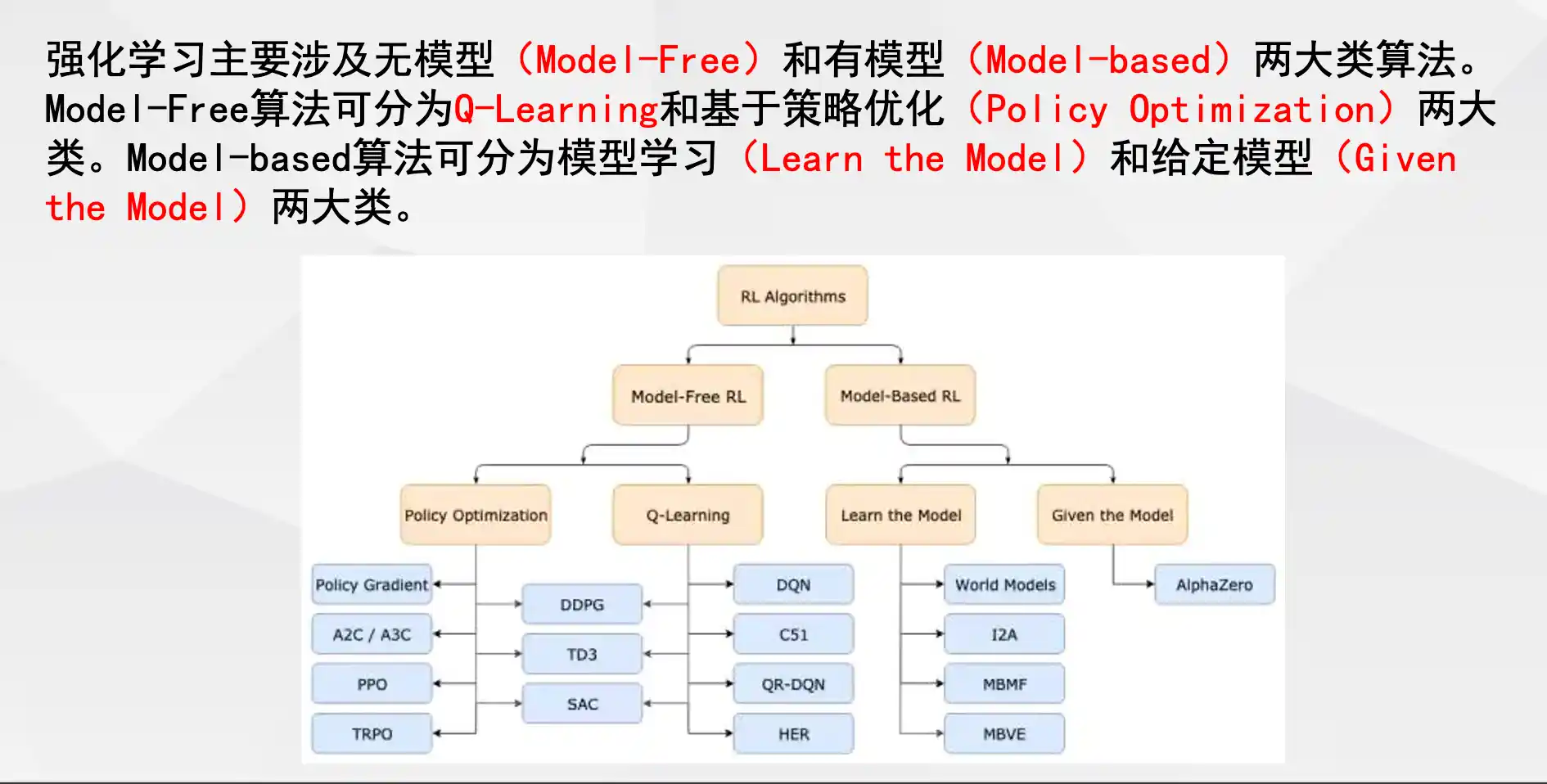
有模型与无模型的区别
| 维度 | 有模型(Model-Based) | 无模型(Model-Free) |
|---|---|---|
| 定义 | 智能体已知环境动态(状态转移概率 ( P_{ss’}^a ) 和奖励函数 ( R_s^a )) | 智能体直接通过与环境的交互学习,无需环境模型 |
| 核心方法 | 动态规划(DP)、值迭代、策略迭代 | 蒙特卡罗(MC)、时序差分(TD)、Q学习、Sarsa |
| 优缺点 | ✅ 样本效率高(无需实际交互) ❌ 依赖精确模型,难以处理复杂环境 |
✅ 适应性强,适用于未知环境 ❌ 样本效率低,收敛慢 |
| 关键步骤 | 1. 构建环境模型 2. 基于模型计算最优策略 |
1. 直接交互获取经验 2. 通过经验更新价值/策略 |
| 典型算法 | 值迭代(Value Iteration)、策略迭代(Policy Iteration) | Q学习(Q-Learning)、Sarsa、REINFORCE |
| 应用场景 | 棋类游戏(已知规则)、仿真环境 | 机器人控制、游戏AI(如Atari) |
定义与核心区别
-
有模型(Model-Based):
- 智能体已知环境模型,即状态转移概率 (P(s’|s,a)) 和奖励函数 (R(s,a))。
- 通过模型进行离线规划(如动态规划),无需与环境实时交互即可优化策略。
- 典型方法:动态规划(DP)、值迭代(Value Iteration)、策略迭代(Policy Iteration)。
- 优点:样本效率高(无需大量试错),适合小规模或已知模型的问题。
- 缺点:模型难以精确获取,复杂环境(如连续状态或高维空间)中不适用。
-
无模型(Model-Free):
- 智能体不依赖环境模型,通过与环境交互直接学习策略或价值函数。
- 通过试错(Trial-and-Error)收集经验,逐步优化策略。
- 典型方法:Q-learning、Sarsa、蒙特卡洛(MC)、深度Q网络(DQN)。
- 优点:适用于未知或复杂环境,更贴近实际应用场景。
- 缺点:样本效率低,训练时间长,可能陷入局部最优。
示例对比
- 迷宫问题:
- 有模型:已知迷宫地图,直接计算最短路径。
- 无模型:通过不断尝试移动并记录奖励,逐步学习最优路径。
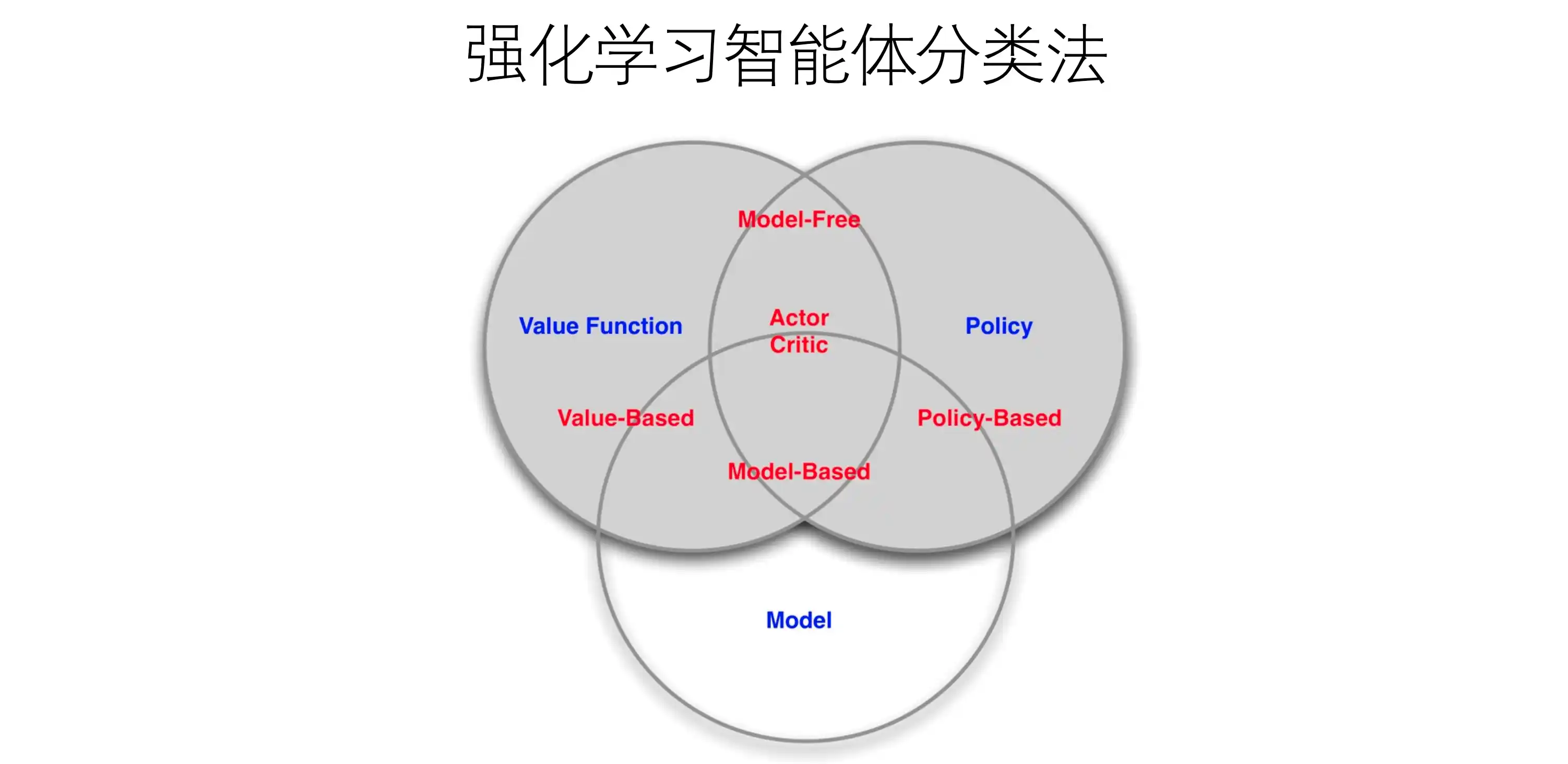
基于价值与基于策略的区别
| 维度 | 基于价值(Value-Based) | 基于策略(Policy-Based) |
|---|---|---|
| 核心目标 | 学习价值函数 ( V(s) ) 或 ( Q(s,a) ),通过价值选择动作(如ε-贪心) | 直接优化策略函数 ( \pi(a|s) ),无需价值函数 |
| 策略类型 | 隐式策略(如贪心策略) | 显式策略(可随机或确定性) |
| 优缺点 | ✅ 适合离散动作空间 ❌ 难以处理高维/连续动作 |
✅ 支持连续动作、随机策略 ❌ 高方差、局部最优 |
| 收敛性 | 可能震荡(如Q学习) | 更平滑但可能陷入局部最优 |
| 典型算法 | Q学习、DQN、Sarsa | REINFORCE、PPO、策略梯度(Policy Gradient) |
| 应用场景 | 离散控制(如Atari游戏) | 连续控制(如机器人行走)、博弈论(如石头剪刀布) |
定义与核心区别
-
基于价值(Value-Based):
- 核心是学习价值函数(如状态价值 (V(s)) 或动作价值 (Q(s,a))),通过选择价值最大的动作间接优化策略。
- 策略通常是隐式的(如 (\epsilon)-贪心策略)。
- 典型方法:Q-learning、Sarsa、DQN。
- 优点:稳定性高,适合离散动作空间。
- 缺点:难以处理高维或连续动作空间,无法学习随机策略。
-
基于策略(Policy-Based):
- 直接学习策略函数 (\pi(a|s)),参数化策略并优化其性能。
- 策略可以是确定性的或随机性的。
- 典型方法:策略梯度(REINFORCE)、PPO(Proximal Policy Optimization)。
- 优点:适合连续动作空间,能学习随机策略(如博弈中的混合策略)。
- 缺点:方差高,收敛速度慢,易陷入局部最优。
示例对比
- 机器人行走:
- 基于价值:计算每个动作的价值,选择最大价值的动作(如关节转动角度)。
- 基于策略:直接输出动作分布(如关节转动的概率),通过梯度上升优化。
混合方法:演员-评论家(Actor-Critic)
- 结合价值函数(Critic)和策略函数(Actor),Critic评估动作价值,Actor优化策略。
- 典型方法:A3C、DDPG。
常用强化学习方法的名称
| 方法名称 | 类型 | 有模型/无模型 | 核心思想 |
|---|---|---|---|
| Q-learning | 基于价值 | 无模型 | 通过最大化Q值更新策略,离线策略(Off-Policy)。 |
| Sarsa | 基于价值 | 无模型 | 在线策略(On-Policy),使用当前策略选择动作。 |
| DQN | 基于价值 | 无模型 | 深度网络近似Q值,引入经验回放和固定目标网络。 |
| 策略梯度(REINFORCE) | 基于策略 | 无模型 | 直接优化策略,通过蒙特卡洛回报计算梯度。 |
| PPO | 基于策略 | 无模型 | 限制策略更新幅度,提升训练稳定性。 |
| Actor-Critic | 混合方法(价值+策略) | 无模型 | Actor输出策略,Critic评估价值,降低方差。 |
| 动态规划(DP) | 基于价值 | 有模型 | 利用环境模型迭代计算最优价值函数。 |
| 蒙特卡洛(MC) | 基于价值 | 无模型 | 通过完整回合的回报更新价值函数。 |
适用场景总结
- 有模型方法:环境模型已知且规模较小(如棋盘游戏、简单控制)。
- 无模型方法:环境复杂或未知(如机器人控制、游戏AI)。
- 基于价值方法:动作空间离散且维度低(如Atari游戏)。
- 基于策略方法:动作空间连续或需要随机策略(如机械臂操控、多智能体博弈)。
详细一点的
1. 动态规划(Dynamic Programming, DP)
- 特点:要求已知MDP模型,通过贝尔曼方程迭代求解。
- 算法:
- 值迭代(Page 63):直接优化值函数 ( V(s) )。
- 策略迭代(Page 60):交替进行策略评估和改进。
2. 无模型方法(Model-Free)
- 蒙特卡罗(MC)(Page 71):
- 通过完整回合的经验更新(如 ( V(s) \leftarrow V(s) + \alpha(G_t - V(s)) ))。
- 高方差但无偏,适用于回合制任务。
- 时序差分(TD)(Page 76):
- TD(0):单步更新(( V(s) \leftarrow V(s) + \alpha(r + \gamma V(s’) - V(s)) ))。
- n-step TD(Page 87):多步混合MC和TD。
- Q学习(Q-Learning)(Page 102):
- 离线策略,更新规则:( Q(s,a) \leftarrow Q(s,a) + \alpha(r + \gamma \max_{a’} Q(s’,a’) - Q(s,a)) )。
- Sarsa(Page 99):
- 在线策略,更新规则:( Q(s,a) \leftarrow Q(s,a) + \alpha(r + \gamma Q(s’,a’) - Q(s,a)) )。
3. 价值函数近似(Value Approximation)
- DQN(Page 126):
- 使用神经网络近似Q函数,引入经验回放和固定目标网络。
- 改进方法:Double DQN、Dueling DQN(Page 133)。
4. 策略优化(Policy Optimization)
- 策略梯度(Page 143):
- REINFORCE(Page 145):蒙特卡罗策略梯度,( \Delta \theta = \alpha \nabla_\theta \log \pi_\theta(s,a) G_t )。
- Actor-Critic(Page 146):
- 结合值函数(Critic)和策略(Actor),如A2C、A3C。